搜索
【题目】在△ABC中,已知∠A+∠B=∠C,则△ABC是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法确定
参考答案：
【答案】A
【解析】解：∠A+∠B=∠C ①
∠A+∠B+∠C=180 ②
联立①②解得∠C=90
则得出△ABC为直角三角形 ；
故应选 ：A 。
根据三角形的内角和及等量代换得出∠C=90 °，根据有一个角是直角的三角形是直角三角形从而得出结论。
-
科目： 来源： 题型：
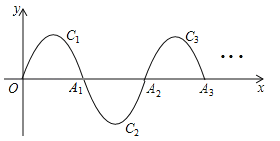
查看答案和解析>>【题目】如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，直至得到C6，若点P（11，m）在第6段抛物线C6上，则m= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果x2-2x-m=0有两个相等的实数根，那么x2-mx-2=0的两根和是_________．
-
科目： 来源： 题型：
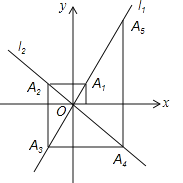
查看答案和解析>>【题目】如图，在平面直角坐标系中，函数y=2x和y=﹣x的图象分别为直线l1，l2，过点（1，0）作x轴的垂线交l2于点A1，过点A1作y轴的垂线交l2于点A2，过点A2作x轴的垂线交l2于点A3，过点A3作y轴的垂线交l2于点A4，…依次进行下去，则点A2017的坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b的图象与反比例函数
（x＞0）的图象交于A（2，﹣1），B（
，n）两点，直线y=2与y轴交于点C．（1）求一次函数与反比例函数的解析式；
（2）求△ABC的面积．
-
科目： 来源： 题型：
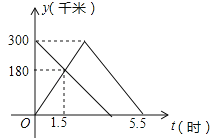
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示
（1）求甲车从A地到达B地的行驶时间；
（2）求甲车返回时y与x之间的函数关系式，并写出自变量x的取值范围；
（3）求乙车到达A地时甲车距A地的路程．
-
科目： 来源： 题型：
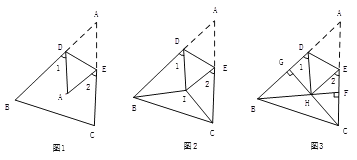
查看答案和解析>>【题目】探究（1）如图1，把△ABC沿DE折叠，使点A落在点A’处，请你判断∠1+∠2与∠A的关系？直接写出结论，不必说明理由.
思考（2）如图2，BI平分∠ABC，CI平分∠ACB，把△ABC折叠，使点A与点I重合，若∠1+∠2=130°，求∠BIC的度数；
应用（3）如图3，在锐角△ABC中，BF⊥AC于点F，CG⊥AB于点G，BF、CG交于点H，把△ABC折叠使点A和点H重合，试探索∠BHC与∠1+∠2的关系，并证明你的结论．
相关试题
