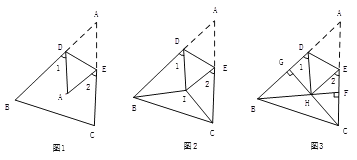
【题目】探究(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A的关系?直接写出结论,不必说明理由.
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
应用(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
参考答案:
【答案】(1)∠1+∠2=2∠A;(2)∠BIC=122.5°;(3)∠BHC=180°﹣![]() (∠1+∠2),理由见解析.
(∠1+∠2),理由见解析.
【解析】试题分析:(1)根据翻折变换的性质以及三角形内角和定理以及平角的定义求出即可;
(2)根据三角形角平分线的性质得出∠IBC+∠ICB=90°-![]() ∠A,得出∠BIC的度数即可;
∠A,得出∠BIC的度数即可;
(3)根据翻折变换的性质以及垂线的性质得出,∠AFH+∠AGH=90°+90°=180°,进而求出∠A=![]() (∠1+∠2),即可得出答案
(∠1+∠2),即可得出答案
试题解析:(1)∠1+∠2=2∠A,
理由:根据翻折的性质,∠ADE=![]() (180°∠1),∠AED=
(180°∠1),∠AED=![]() (180°∠2),
(180°∠2),
∵∠A+∠ADE+∠AED=180°,
∴∠A+![]() (180°∠1)+
(180°∠1)+![]() (180°∠2)=180°,
(180°∠2)=180°,
整理得2∠A=∠1+∠2;
(2)由(1)∠1+∠2=2∠A,得2∠A=130°,
∴∠A=65°
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣![]() ∠A,
∠A,
∴∠BIC=180°﹣(∠IBC+∠ICB)=180°﹣(90°﹣![]() ∠A)=90°+
∠A)=90°+![]() ×65°=122.5°;
×65°=122.5°;
(3)∠BHC=180°﹣![]() (∠1+∠2).
(∠1+∠2).
理由:∵BF⊥AC,CG⊥AB,
∴∠AFH+∠AGH=90°+90°=180°,∠FHG+∠A=180°,
∴∠BHC=∠FHG=180°﹣∠A,
由(1)知∠1+∠2=2∠A,
∴∠A=![]() (∠1+∠2),
(∠1+∠2),
∴∠BHC=180°﹣![]() (∠1+∠2).
(∠1+∠2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知∠A+∠B=∠C,则△ABC是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数
 (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.

-
科目: 来源: 题型:
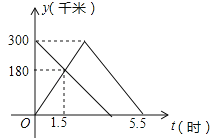
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程2x2﹣2=0的解是 .
-
科目: 来源: 题型:
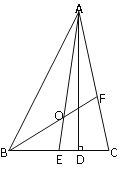
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC及∠BOA的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组长度的线段能构成直角三角形的一组是( )
A.30,40,50
B.7,12,13
C.5,9,12
D.3,4,6
相关试题

