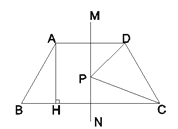
【题目】如图,题型ABCD中,AD∥BC,AD=CD=AD=2,∠B=60°,AH⊥BC于点H,且AH=![]() ,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
参考答案:
【答案】![]()
【解析】试题解析:连接AC交直线MN于P点,P点即为所求.
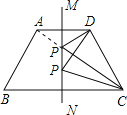
∵直线MN为梯形ABCD的对称轴,
∴AP=DP,
∴当A、P、C三点位于一条直线时,PC+PD=AC,为最小值,
∵AD=DC=AB,AD∥BC,
∴∠DCB=∠B=60°,
∵AD∥BC,
∴∠ACB=∠DAC,
∵AD=CD,
∴∠DAC=∠DCA,
∴∠DAC=∠DCA=∠ACB
∵∠ACB+∠DCA=60°,
∴∠DAC=∠DCA=∠ACB=30°,
∴∠BAC=90°,
∵AB=2,∠B=60°
∴AC=tan60°×AB=![]() ×2=2
×2=2![]() .
.
∴PC+PD的最小值为2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.x4x2=x8
B.x4÷x2=x6
C.(x4)2=x8
D.(3x)2=3x2 -
科目: 来源: 题型:
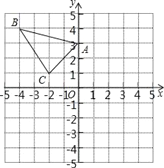
查看答案和解析>>【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,能使用平方差公式计算的是( )
A.(a﹣1)2B.(a+1)2
C.(a+1)(a﹣1)D.(﹣a+1)(a﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(m,﹣n)在第二象限,则点B(﹣m,|n|)在第_____象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:x(x﹣2)=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=2,an=3,则am+n的值是_____.
相关试题

