【题目】如图已知:![]() 点
点![]() ···,在射线
···,在射线![]() 上,点
上,点![]() ,···,在射线
,···,在射线![]() 上,
上,![]() ,···,均为等边三角形,若
,···,均为等边三角形,若![]() 则
则![]() 的边长为________________________.
的边长为________________________.
参考答案:
【答案】128
【解析】
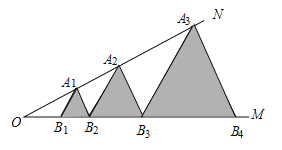
根据等腰三角形的性质以及平行线的性质得出B1A1//A2B2//A3B3,以及a2=2a1,得出a3=4a1=4,a4=8a1=8,a5=16a1…进而得出答案.
解:∵△A1B1B2是等边三角形,
∴∠A1B1B2=∠A1B2O=60°,A1B1=A1B2,
∵∠O=30°,
∴∠A2A1B2=∠O+∠A1B2O=90°,
∵∠A1B1B2=∠O+∠OA1B1,
∴∠O=∠OA1B1=30°,
∴OB1=A1B1=A1B2=1,
在Rt△A2A1B2中,∵∠A1A2B2=30°,
∴A2B2=2A1B2=2,
同法可得A3B3=22,A4B4=23,…,AnBn=2n﹣1,
∴△A8B8B9的边长=27=128,
故答案为:128.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
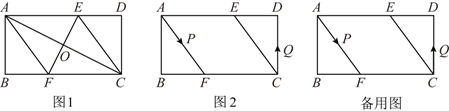
(1)如图1,连接AF、CE求证:四边形AFCE为菱形;
(2)如图1,求AF的长;
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2+bx+c=0变形为:
x2+
 x=﹣
x=﹣ ,…第一步
,…第一步x2+
 x+(
x+( )2=﹣
)2=﹣ +(
+( )2,…第二步
)2,…第二步(x+
 )2=
)2= ,…第三步
,…第三步x+
 =
= (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步x=
 ,…第五步
,…第五步嘉淇的解法从第 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
-
科目: 来源: 题型:
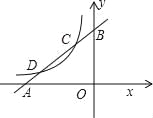
查看答案和解析>>【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线
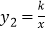 (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1>y2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)
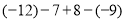
(2)

(3)
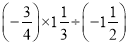
(4)
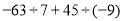
(5)
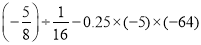
(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位在疫情期间用
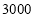 元购进
元购进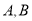 两种口罩
两种口罩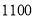 个,购买
个,购买 种口罩与购买
种口罩与购买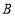 种口罩的费用相同,且
种口罩的费用相同,且 种口罩的单价是
种口罩的单价是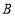 种口罩单价的
种口罩单价的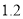 倍.
倍.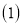 求
求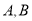 两种口罩的单价各是多少元?
两种口罩的单价各是多少元?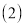 若计划用不超过
若计划用不超过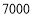 元的资金再次购进
元的资金再次购进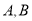 两种口罩共
两种口罩共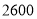 个,已知
个,已知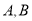 两种口罩的进价不变,求
两种口罩的进价不变,求 种口罩最多能购买多少个?
种口罩最多能购买多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件;现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.现在要使每星期利润为6125元,设每件商品应降价x元,则可列方程为( )
A. (20+x)(300+20x)=6125 B. (20-x)(300-20x)=6125
C. (20-x)(300+20x)=6125 D. (20+x)(300-20x)=6125
相关试题

