【题目】某单位在疫情期间用![]() 元购进
元购进![]() 两种口罩
两种口罩![]() 个,购买
个,购买![]() 种口罩与购买
种口罩与购买![]() 种口罩的费用相同,且
种口罩的费用相同,且![]() 种口罩的单价是
种口罩的单价是![]() 种口罩单价的
种口罩单价的![]() 倍.
倍.
![]() 求
求![]() 两种口罩的单价各是多少元?
两种口罩的单价各是多少元?
![]() 若计划用不超过
若计划用不超过![]() 元的资金再次购进
元的资金再次购进![]() 两种口罩共
两种口罩共![]() 个,已知
个,已知![]() 两种口罩的进价不变,求
两种口罩的进价不变,求![]() 种口罩最多能购买多少个?
种口罩最多能购买多少个?
参考答案:
【答案】(1)A口罩单价为3元/个,B口罩单价为2.5元/个;(2)A种口罩最多能购进1000个.
【解析】
(1)设B口罩的单价为x元/个,则A口罩单价为1.2x元/个,根据数量=总价÷单价结合用3000元购进A、B两种口罩1100个,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)购进A口罩m个,则购进B口罩(2600m)个,根据总价=单价×数量结合总价不超过7000元,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出结论.
解:(1)设B口罩的单价为x元/个,则A口罩单价为1.2x元/个,
根据题意得:![]()
解得:x=2.5,
经检验,x=2.5是原方程的解,且符合题意,
则1.2x=3,
答:A口罩单价为3元/个,B口罩单价为2.5元/个;
(2)设购进A口罩m个,则购进B口罩(2600m)个,
依题意,得:3m+2.5(2600m)≤7000,
解得:m≤1000,
答:A种口罩最多能购进1000个.
-
科目: 来源: 题型:
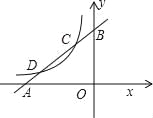
查看答案和解析>>【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线
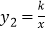 (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1>y2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知:
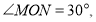 点
点 ···,在射线
···,在射线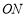 上,点
上,点 ,···,在射线
,···,在射线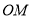 上,
上, ,···,均为等边三角形,若
,···,均为等边三角形,若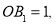 则
则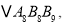 的边长为________________________.
的边长为________________________.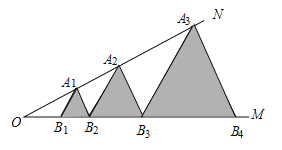
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)
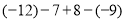
(2)

(3)
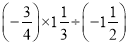
(4)
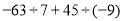
(5)
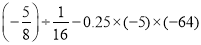
(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件;现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.现在要使每星期利润为6125元,设每件商品应降价x元,则可列方程为( )
A. (20+x)(300+20x)=6125 B. (20-x)(300-20x)=6125
C. (20-x)(300+20x)=6125 D. (20+x)(300-20x)=6125
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
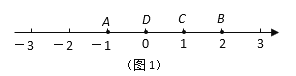
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.
(1)数_______________________ 所表示的点是(M,N)的好点;
(2)数________________________ 所表示的点是(N,M)的好点;

(温馨提示:注意考虑M,N的左侧、右侧,不要漏掉答案)
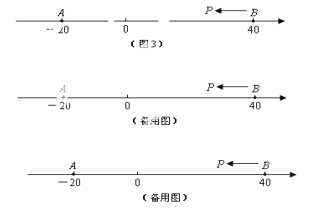
(3)如图(3)A,B为数轴上的两点,点A所表示的数为-20,点B表示的数为 40,现有一只电子蚂蚁P从点B出发,以2单位每秒的速度一直向左运动,
①当t为何值时,P是(A,B)的好点?
②当t为何值时,P是(B,A)的好点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为__m.

相关试题

