【题目】计算题:
(1) ![]()
(2)![]()
(3)![]()
(4)![]()
(5) ![]()
(6) ![]()
参考答案:
【答案】(1)-2;(2)-10.5;(3)![]() ;(4)-14;(5)-90;(6)-300
;(4)-14;(5)-90;(6)-300
【解析】
(1)原式利用有理数的加减法法则,计算即可求出值;
(2)原式利用有理数的加减法法则,计算即可求出值;
(3)原式利用有理数的乘除法法则,计算即可求出值;
(4)原式先算除法,然后利用有理数加法法则,计算即可求出值;
(5)原式先算乘、除法,然后利用有理数加法法则,计算即可求出值;
(6)原式先算括号里的,然后利用有理数除法法则,计算即可求出值;
解:(1)原式=-12-7+8+9=-2
(2)原式=-0.5-15+17-12=-10.5
(3)原式=![]()
(4)原式=-9+(-5)=-14
(5)原式=![]()
(6)原式=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2+bx+c=0变形为:
x2+
 x=﹣
x=﹣ ,…第一步
,…第一步x2+
 x+(
x+( )2=﹣
)2=﹣ +(
+( )2,…第二步
)2,…第二步(x+
 )2=
)2= ,…第三步
,…第三步x+
 =
= (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步x=
 ,…第五步
,…第五步嘉淇的解法从第 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
-
科目: 来源: 题型:
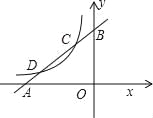
查看答案和解析>>【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线
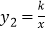 (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1>y2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知:
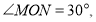 点
点 ···,在射线
···,在射线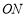 上,点
上,点 ,···,在射线
,···,在射线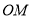 上,
上, ,···,均为等边三角形,若
,···,均为等边三角形,若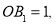 则
则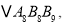 的边长为________________________.
的边长为________________________.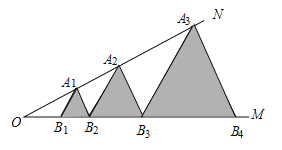
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位在疫情期间用
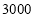 元购进
元购进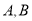 两种口罩
两种口罩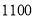 个,购买
个,购买 种口罩与购买
种口罩与购买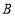 种口罩的费用相同,且
种口罩的费用相同,且 种口罩的单价是
种口罩的单价是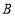 种口罩单价的
种口罩单价的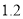 倍.
倍.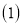 求
求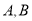 两种口罩的单价各是多少元?
两种口罩的单价各是多少元?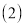 若计划用不超过
若计划用不超过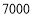 元的资金再次购进
元的资金再次购进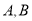 两种口罩共
两种口罩共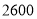 个,已知
个,已知 两种口罩的进价不变,求
两种口罩的进价不变,求 种口罩最多能购买多少个?
种口罩最多能购买多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件;现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.现在要使每星期利润为6125元,设每件商品应降价x元,则可列方程为( )
A. (20+x)(300+20x)=6125 B. (20-x)(300-20x)=6125
C. (20-x)(300+20x)=6125 D. (20+x)(300-20x)=6125
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
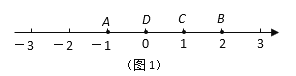
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.
(1)数_______________________ 所表示的点是(M,N)的好点;
(2)数________________________ 所表示的点是(N,M)的好点;

(温馨提示:注意考虑M,N的左侧、右侧,不要漏掉答案)
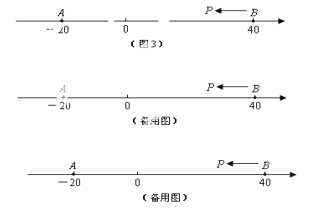
(3)如图(3)A,B为数轴上的两点,点A所表示的数为-20,点B表示的数为 40,现有一只电子蚂蚁P从点B出发,以2单位每秒的速度一直向左运动,
①当t为何值时,P是(A,B)的好点?
②当t为何值时,P是(B,A)的好点?
相关试题

