【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= ![]() 在第一象限内的图象交于点P,且△POA的面积为2.
在第一象限内的图象交于点P,且△POA的面积为2.
(1)求k的值.
(2)求平移后的直线的函数解析式.
参考答案:
【答案】
(1)解:∵点A(m,2)在直线y=2x,
∴2=2m,
∴m=1,
∴点A(1,2),
∵点A(1,2)在反比例函数y= ![]() 上,
上,
∴k=2
(2)解:如图,

设平移后的直线与y轴相交于B,过点P作PM⊥OA,BN⊥OA,AC⊥y轴
由(1)知,A(1,2),
∴OA= ![]() ,sin∠BON=sin∠AOC=
,sin∠BON=sin∠AOC= ![]() =
= ![]() ,
,
∵S△POA= ![]() OA×PM=
OA×PM= ![]() ×
× ![]() PM=2,
PM=2,
∴PM= ![]() ,
,
∵PM⊥OA,BN⊥OA,
∴PM∥BN,
∵PB∥OA,
∴四边形BPMN是平行四边形,
∴BN=PM= ![]() ,
,
∵sin∠BON= ![]() =
= ![]() =
= ![]() ,
,
∴OB=4,
∵PB∥AO,
∴B(0,﹣4),
∴平移后的直线PB的函数解析式y=2x﹣4
方法二、如图1,过点P作PC⊥y轴交OA于C,
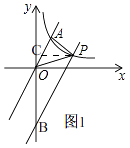
设点P的坐标为(n, ![]() )(n>1),
)(n>1),
∴C( ![]() ,
, ![]() ),∴PC=n﹣
),∴PC=n﹣ ![]() ,
,
∵△POA的面积为2.A(1,2)
∴S△POA=S△PCO+S△PCA
= ![]() (n﹣
(n﹣ ![]() )×
)× ![]() +
+ ![]() (n﹣
(n﹣ ![]() )(2﹣
)(2﹣ ![]() )
)
= ![]() (n﹣
(n﹣ ![]() )×2
)×2
=n﹣ ![]()
=2,
∴n=1﹣ ![]() (舍)或n=1+
(舍)或n=1+ ![]() ,
,
∴P(1+ ![]() ,2
,2 ![]() ﹣2)
﹣2)
∴PB∥AO,
∴设直线PB的解析式为y=2x+b,
∵点P在直线PB上,
∴2 ![]() ﹣2=2(1+
﹣2=2(1+ ![]() )+b,
)+b,
∴b=﹣4,
∴平移后的直线PB的函数解析式y=2x﹣4,
【解析】(1)由点A的纵坐标求得m,即点A的坐标,把A点的坐标代入反比例函数中即可;(2)先求出PM,再求出BN然后用锐角三角函数求得OB即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,
中, 厘米,
厘米, ,
,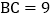 厘米,点D为AB的中点
厘米,点D为AB的中点 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米 秒,则当
秒,则当 与
与 全等时,v的值为
全等时,v的值为

A.
 B. 3 C.
B. 3 C.  或3 D. 1或5
或3 D. 1或5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β;②α-β;③β-α;④180°-α-β中.∠AEC的度数可能是 _____(把正确答案的序号填在横线上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行“建国70周年”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如下不完整的两幅统计图表.


请根指以上信息,解答下列问题
(1)征文比赛成绩频数分布表中,a= ,b= ,c= .
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市民居民“一户一表”生活用水阶梯式计费价格表的部分信息:

(说明:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费)
已知小王家2012年4月用水20吨,交水费66元,5月份用水25吨,交水费91元.
(1)求a,b的值;
(2)随着夏天的到来,用水量将增加.为了节省开支.小王计划把6月份的水费控制在不超过家庭月收入的2%,若小王家的月收入为9200元,则小王家6月份最多能用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
相关试题

