【题目】如图,抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7)且与直线y=kx﹣2k﹣3相交于点P(m,2m﹣7). 
(1)求抛物线的解析式;
(2)求直线y=kx﹣2k﹣3与抛物线y=ax2﹣(2a+1)x+b的对称轴的交点Q的坐标;
(3)在y轴上是否存在点T,使△PQT的一边中线等于该边的一半?若存在,求出点T的坐标;若不存在请说明理由.
参考答案:
【答案】
(1)解:∵抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7),
∴ ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为y= ![]() x2﹣2x+1
x2﹣2x+1
(2)解:∵抛物线的图象经过点P(m,2m﹣7),
∴2m﹣7= ![]() m2﹣2m+1,
m2﹣2m+1,
解得m1=m2=4,
∴点P的坐标为(4,1),
∵直线y=kx﹣2k﹣3经过点P,
∴4k﹣2k﹣3=1,
解得k=2,
∴直线的解析式为y=2x﹣7,
∵y= ![]() x2﹣2x+1=
x2﹣2x+1= ![]() (x﹣2)2﹣1,
(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,
∴在y=2x﹣7中,当x=2时,y=2×2﹣7=﹣3,
∴点Q的坐标为(2,﹣3)
(3)解:设点T的坐标为(0,t),M为PQ的中点,连结TM,根据题意得:
TM= ![]() PQ,即TM=PM=QM,
PQ,即TM=PM=QM,
∴点T在以PQ为直径的圆上,
∴∠PTQ=90°,
∴△PQT为直角三角形,
同理,点M为PT或QT的中点时,△PQT仍为直角三角形,
作PA⊥y轴于A,交直线x=2于点C,QB⊥y轴于B,则AT=|1﹣t|,BT=|﹣3﹣t|,
∵PA=4,QB=2,PC=2,CQ=4,
∴PQ= ![]() =
= ![]() =2
=2 ![]() ,
,
①当∠PTQ=90°时,
∵PQ2=TQ2+TP2=BT2+QB2+PA2+AT2
=|﹣3﹣t|2+22+|1﹣t|2+42=20,
∴2t2+4t+10=0,即(t+1)2=﹣4,
∵(t+1)2≥0,
∴此方程无解;
②当∠PQT=90°时,PQ2+QT2=PT2,
∴(2 ![]() )2+22+|﹣3﹣t|2=42+|1﹣t|2,
)2+22+|﹣3﹣t|2=42+|1﹣t|2,
解得t=﹣2;
③当∠QPT=90°时,TQ2=PT2+PQ2,
∴QB2+BT2=PA2+AT2+(2 ![]() )2,
)2,
∴4+|﹣3﹣t|2=16+|1﹣t|2+20,
解得t=3,
综上所述,在y轴上存在点T,其坐标分别为(0,3)和(0,﹣2),使△PQT的一边中线等于该边的一半.
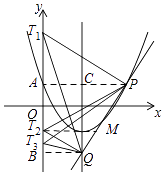
【解析】(1)根据抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7),求得a,b的值即可得到抛物线的解析式;(2)先根据抛物线的图象经过点P(m,2m﹣7),求得点P的坐标,再根据直线y=kx﹣2k﹣3经过点P,求得k的值,最后根据抛物线的对称轴为直线x=2,求得点Q的坐标;(3)设点T的坐标为(0,t),M为PQ的中点,连结TM,分三种情况讨论:∠PTQ=90°时,∠PQT=90°时,∠QPT=90°时,分别根据勾股定理列出关于t的方程进行求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:
(1)
 ,其中
,其中 ;
;(2)若
 ,且
,且 ,求
,求 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
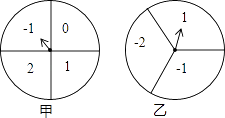
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.

(1)当α=60°时(如图1), ①判断△ABC的形状,并说明理由;
②求证:BD= AE;
AE;
(2)当α=90°时(如图2),求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
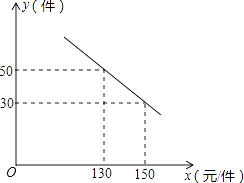
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
相关试题

