【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

参考答案:
【答案】(1)证明见解析;(2)69°.
【解析】试题分析:(1)根据已知条件易证∠BEO=∠1,根据等式的性质可得∠AEC=∠BED,利用ASA即可证明△AEC≌△BED;(2)由△AEC≌△BED可得EC=ED,∠C=∠BDE;在△EDC中,根据等腰三角形的性质和三角形的内角和定理可求得∠C的度数,根据全等三角形的性质即可求得∠BDE的度数.
试题解析:
(1)证明:∵AE和BD相交于点O, ∴∠AOD=∠BOE.
在△AOD和△BOE中, ∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO, ∴∠AEC=∠BED.
在△AEC和△BED中,
∠A=∠B,AE=BE,∠AEC=∠BED,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中, ∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°,
∴∠BDE=∠C=69°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-x5·x2·x10;
(2)(-2)9×(-2)8×(-2)3;
(3)a6·a2+a5·a3-2a·a7;
(4)(-a)2·(-a)3·a6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC=2
 ,sinB=
,sinB= ,D为边BC的中点,E为边BC的延长线上一点,且CE=BC,连结AE,F为线段AE的中点.
,D为边BC的中点,E为边BC的延长线上一点,且CE=BC,连结AE,F为线段AE的中点.求:(1)线段DE的长;(2)tan∠CAE的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解决问题
平面内的两条直线相交和平行两种位置关系,如图①,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,所以∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.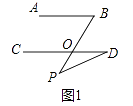
(1)将点P移到AB、CD内部,其余条件不变,如图②,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;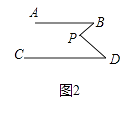
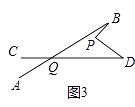
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,能否借助(1)中的图形与结论,找出图③中∠BPD、∠B、∠D、∠BQD之间有何数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4x+1=0的根的情况是( )
A.没有实数根
B.只有一个实数根
C.有两个相等的实数根
D.有两个不相等的实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在“五一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:①如果不超过500元,则不予优惠;②如果超过500元,但不超过800元,则按购物总额给予8折优惠;③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款480元和520元;若合并付款,则她们总共只需付款元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)等腰三角形一腰上的中线将这个等腰三角形的周长分成15 cm和6 cm两部分.求等腰三角形的底边长.

(2)已知等腰三角形中,有一个角比另一个角的2倍少20°,求顶角的度数
相关试题

