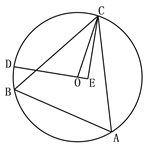
【题目】如图,△ABC为⊙O的内接三角形,BC=24 , ![]() ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
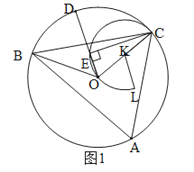
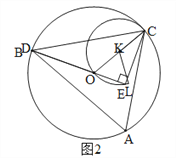
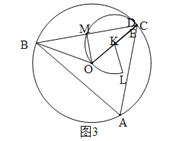
【解析】解:当点D由B点沿弧BC运动到点C时,点E经过的路径是以OC的中点K为圆心,以![]() OC为半径的一段圆弧,圆心角为240°,如图1.当D与B重合时,如图2,E和L重合.∵∠A=60°,∴∠BOC=120°,∴∠COE=60°.∵OK=KL,∴△OKL是等边三角形,∴∠OKL=60°.当D运动到C时,如图3,D、E、C三点重合,此时∠OKC=180°,∴∠LKC=60°+180°=240°.过O作OM⊥BC于M,如图3,则BM=
OC为半径的一段圆弧,圆心角为240°,如图1.当D与B重合时,如图2,E和L重合.∵∠A=60°,∴∠BOC=120°,∴∠COE=60°.∵OK=KL,∴△OKL是等边三角形,∴∠OKL=60°.当D运动到C时,如图3,D、E、C三点重合,此时∠OKC=180°,∴∠LKC=60°+180°=240°.过O作OM⊥BC于M,如图3,则BM=![]() BC=12.∵∠BOC=120°,OB=OC,∴∠MBO=(180°-120°)÷2=30°,∴OM=
BC=12.∵∠BOC=120°,OB=OC,∴∠MBO=(180°-120°)÷2=30°,∴OM=![]() ,OB=2OM=
,OB=2OM=![]() ,∴OK=
,∴OK=![]() OB=
OB=![]() ,∴点E经过的路径长为
,∴点E经过的路径长为![]() =
=![]() .故选C.
.故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为AB边上一点,E为CD中点,AC=
 ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
A.
 B.
B.  +1﹣
+1﹣ C.
C.  ﹣
﹣ D.
D.  ﹣1
﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
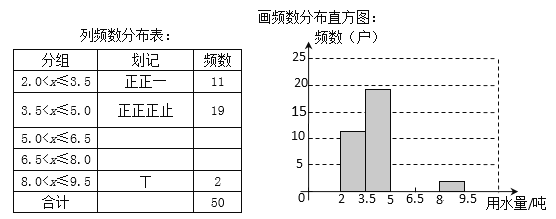
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量y(件)与该商品定价x(元)是一次函数关系,如图所示.
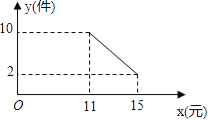
(1)求销售量y与定价x之间的函数关系式;
(2)如果超市将该商品的销售价定为13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:﹣32+|2﹣5|÷
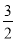 +(﹣2)3×(﹣1)2015
+(﹣2)3×(﹣1)2015 (2)解方程:
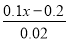 ﹣
﹣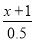 =3.
=3. (3)解方程:6(x-2)=8x+3.
(4)解方程: x-
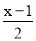 =2-
=2-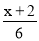 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生
A
B
C
D
E
F
身高(单位:cm)
165
____
166
____
____
172
身高与班级平
均身高的差值)
-1
+2
____
-3
+4
____
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解决有关问题:
我们知道,|m|=
 .现在我们可以用这一结论来化简含有绝对值的代
.现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|m+1|+|m﹣2|时,可令 m+1=0 和 m﹣2=0,分别求得 m=﹣1,m=2(称﹣1,2 分别为|m+1|与|m﹣2|的零点值).在实数范围内, 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况:
(1)当 m<﹣1 时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2 时,原式=m+1﹣(m﹣2)=3;
(3)当 m≥2 时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=

通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
相关试题

