【题目】如图1,直线l : ![]() 经过定点P,交x、y轴于A、B两点.
经过定点P,交x、y轴于A、B两点.
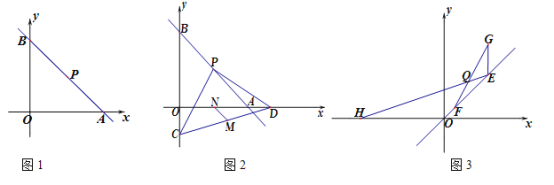
(1)如图1,直接写出点P的坐标__________________;
(2)如图2,当k=—1时,点C为y轴负半轴上一动点,过点P作PD⊥PC交x轴于点D,M、N分别为CD、OA的中点,求![]() 的值;
的值;
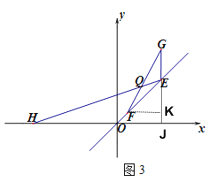
(3)如图3,E、F两点在射线OP上移动,EF=![]() ,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
参考答案:
【答案】(1)(2,2);(2)![]() ;(3)点Q在直线
;(3)点Q在直线![]() 上运动.
上运动.
【解析】
(1)将直线l解析式变形可得到定点坐标;
(2)过点P作EF∥x轴,过点D作DF⊥EF垂足为F,首先证明△EPC≌△FDP,设C(0,m),则PF=CE=2-m,易得D(4-m,0),然后根据k=-1求出A点坐标,可得AD=-m,利用中点坐标公式和两点间距离公式求出MN,问题得解;
(3)如图3,延长GE交x轴于点J,则GJ⊥x轴,过点F作FK⊥GJ于点K,由OP所以直线解析式为y=x,可求得F点、G点坐标,然后用待定系数法求出直线HE和直线FG解析式,求出交点Q的坐标,即可解得点Q在直线![]() 上运动.
上运动.
解:(1)∵![]() ,
,
∴当x=2时,y=2,
∴定点P的坐标是(2,2);
(2)如图2,过点P作EF∥x轴,过点D作DF⊥EF垂足为F,
∵P(2,2),∴PE=OE=DF=2,
∵PD⊥PC,
∴∠EPC+∠FPD=90°,
∵∠EPC+∠ECP=90°,
∴∠FPD=∠ECP,
在△EPC和△FDP中,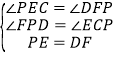 ,
,
∴△EPC≌△FDP(AAS),
∴PF=CE,
设C(0,m),则PF=CE=2-m,
∴OD=PE+PF=4-m,
∴D(4-m,0),
当k=-1时,直线l解析式为:![]() ,
,
∴A(4,0),AD=-m,
∵M、N分别为CD、OA的中点,
∴M(![]() ,
,![]() ),N(2,0),
),N(2,0),
∴MN=![]() ,
,
∴![]() ;
;
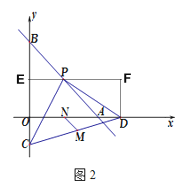
(3)如图3,延长GE交x轴于点J,则GJ⊥x轴,过点F作FK⊥GJ于点K,
∵E、F两点在射线OP上移动且P(2,2),
∴OP所以直线解析式为:y=x,
∴∠EOJ=∠EFK =45°,
∵EF=![]() ,
,
∴EK=FK=EG=2,
∵E(t,t),
∴G(t,t+2),F(t-2,t-2),
设直线HE解析式为:y=kx+b(k≠0),
将点E(t,t),H(-2t,0)代入可得:![]() ,
,
解得: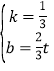 ,
,
∴直线HE解析式为:y=![]() x+
x+![]() ,
,
设直线FG解析式为:y=k1x+b1(k≠0),
将点 G(t,t+2),F(t-2,t-2)代入可得:![]() ,
,
解得:![]() ,
,
∴直线FG解析式为:y=2x+2-t,
联立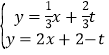 ,解得:
,解得: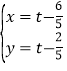 ,
,
即Q(![]() ,
,![]() ),
),
∵![]() ,
,
∴点Q在直线![]() 上运动.
上运动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=
 交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2
交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2 ,OA=OB=1.
,OA=OB=1.
(1)△ADC 的面积;
(2)求反比例函数y=
 与一次函数的y=k1x+b表达式.
与一次函数的y=k1x+b表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】松雷中学图书馆近日购进甲、乙两种图书,每本甲图书的进价比每本乙图书的进价高20元,花780元购进甲图书的数量与花540元购进乙图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元?
(2)松雷中学计划购进甲、乙两种图书共70本,总购书费用不超过4000元,则最多购进甲种图书多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆的直径,过圆心O作AB的垂线,与弦AC的延长线交于点D,点E在OD上
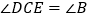 .
.(1)求证:CE是半圆的切线;
(2)若CD=10,
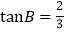 ,求半圆的半径.
,求半圆的半径.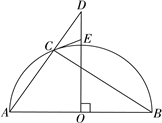
-
科目: 来源: 题型:
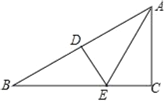
查看答案和解析>>【题目】如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB和BC于点D,E,且AE平分∠BAC.
(1)求∠C的度数;
(2)若CE=1,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见下图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意两个实数对(a,b)和(c,d),规定:当且仅当a=c且b=d时, (a,b)=(c,d).定义运算“
 ”:(a,b)
”:(a,b) (c,d)=(ac-bd,ad+bc).若(1,2)
(c,d)=(ac-bd,ad+bc).若(1,2) (p,3)=(q,q),则pq=___________.
(p,3)=(q,q),则pq=___________.
相关试题

