搜索
【题目】如图，在正方形ABCD中，E为 BC上的点，F为 CD边上的点，且AE=AF，AB=4，设EC=x，△AEF 的面积为y，则y与x之间的函数关系式是____.
参考答案：
【答案】y=-
x2+4x．
【解析】
试题根据正方形的性质可得AB=AD，再利用“HL”证明Rt△ABE和Rt△ADF全等，根据全等三角形对应边相等可得BE=DF，然后求出CE=CF，再根据△AEF的面积等于正方形的面积减去三个直角三角形的面积列式整理即可得解．
试题解析：在正方形ABCD中，AB=AD，
在Rt△ABE和Rt△ADF中，
，
∴Rt△ABE≌Rt△ADF（HL），
∴BE=DF，
∴CE=CF，
∵CE=x，
∴BE=DF=4-x，
∴y=42-2××4×（4-x）-x2，
=-x2+4x，
即y=-x2+4x．
-
科目： 来源： 题型：
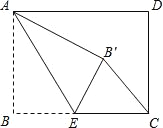
查看答案和解析>>【题目】矩形ABCD中，AB＝3，BC＝4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为( )
A. 3 B.
C. 2或3 D. 3或 -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y＝ax2+bx+c的图象如图所示，以下结论：①abc＞0；②4ac＜b2；③2a+b＞0；④其顶点坐标为(
，﹣2)；⑤当x＜时，y随x的增大而减小；⑥a+b+c＞0中，其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD的面积为10cm2，它的两条对角线交于点O1，以AB、AO1为两邻边作平行四边形ABC1O1，平行四边形ABC1O1的对角线交于点O2，同样以AB、AO2为两邻边作平行四边形ABC2O2，…，依此类推，则平行四边形ABCnOn的面积为( )
A.
cm2B.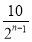 
cm2C. 
cm2D. 
cm2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将边长为
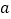的正方形的边长增加
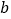，得到一个边长为
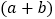的正方形.在图1的基础上，某同学设计了一个解释验证
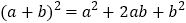的方案（详见方案1）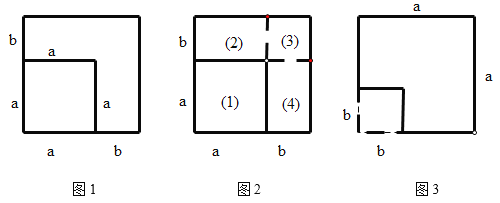
方案1.如图2，用两种不同的方式表示边长为
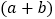的正方形的面积.方式1：
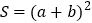
方式2：
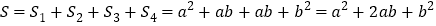
因此，
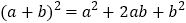
（1）请模仿方案1，在图1的基础上再设计一种方案，用以解释验证
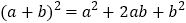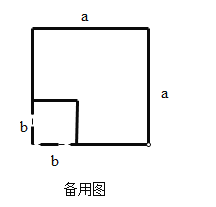
；（2）如图3，在边长为
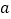的正方形纸片上剪掉边长为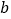的正方形，请在此基础上再设计一个方案用以解释验证
. -
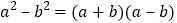科目： 来源： 题型：
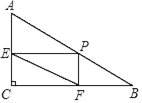
查看答案和解析>>【题目】如图，Rt△ABC中，∠C=90°，AC=3，BC=4，点P为AB边上任一点，过P分别作PE⊥AC于E，PF⊥BC于F，则线段EF的最小值是__________．
-
科目： 来源： 题型：
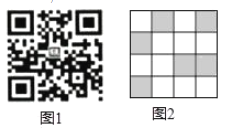
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别，某校建立了一个身份识别系绕，图2是某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0，将第一行数字从左到右依次记为a，b，c，d，那么可以转换为该生所在班级序号，其序号为a×23+b×22+c×21+d×20，如图2第一行数字从左到右依次为0，1，0，1，序号为0×23+1×22+0×21+1×20＝5，表示该生为5班学生，那么表示7班学生的识别图案是( )
A.
B.
C.
D.
相关试题
