【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
A. 3 B. ![]() C. 2或3 D. 3或
C. 2或3 D. 3或![]()
参考答案:
【答案】D
【解析】
当△CEB′为直角三角形时,有两种情况:
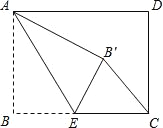
①当点B′落在矩形内部时,如图1所示.
连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.
②当点B′落在AD边上时,如图2所示.此时ABEB′为正方形.
当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如图1所示.
连结AC,
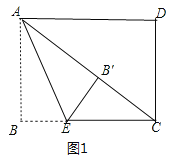
在Rt△ABC中,AB=3,BC=4,
∴AC=![]() =5,
=5,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5-3=2,
设BE=x,则EB′=x,CE=4-x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+22=(4-x)2,解得x=![]() ,
,
∴BE=![]() ;
;
②当点B′落在AD边上时,如图2所示.
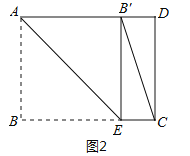
此时ABEB′为正方形,
∴BE=AB=3.
综上所述,BE的长为![]() 或3.
或3.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四个螺丝将四条不可弯曲的本条围成一个木框(形状不限),不记螺丝大小,其中相邻两螺丝之间的距离依次为3,4,5,7.且相邻两本条的夹角均可调整,若调整木条的夹角时不破坏此木框,则任意两个螺丝之间的最大距离是( )
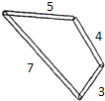
A.6B.7C.8D.9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
-
科目: 来源: 题型:
查看答案和解析>>【题目】春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用152元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A型放大镜?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图一:
 中,
中, 平分
平分 ,CO平分外角
,CO平分外角 .
.(1)①若
 ,则
,则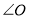 的度数为________.
的度数为________.②若
 ,则
,则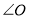 的度数为________.
的度数为________.(2)试写出
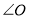 与
与 的关系,并加以证明.
的关系,并加以证明.(3)解决问题,如图二,
 平分
平分 ,
, 平分
平分 , 依此类推,
, 依此类推, 平分
平分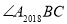 ,
, 平分
平分 ,
, 平分
平分 , 依此类推,
, 依此类推, 平分
平分 ,若
,若 ,请根据第(2)间中得到的结论直接写出
,请根据第(2)间中得到的结论直接写出 的度数为________.
的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A. y=﹣(x﹣
 )2﹣
)2﹣ B. y=﹣(x+
B. y=﹣(x+ )2﹣
)2﹣
C. y=﹣(x﹣
 )2﹣
)2﹣ D. y=﹣(x+
D. y=﹣(x+ )2+
)2+
相关试题

