【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.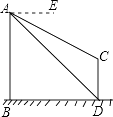
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
参考答案:
【答案】
(1)解:根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)解:延长AE、DC交于点F,
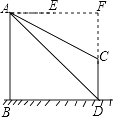
根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
∴CF=AFtan∠FAC=60× ![]() =20
=20 ![]() ,
,
又∵FD=60,
∴CD=60﹣20 ![]() ,
,
∴建筑物CD的高度为(60﹣20 ![]() )米.
)米.
【解析】(1)根据题意得:BD∥AE,然后根据平行线的性质的出∠ADB=∠EAD=45°,从而根据三角形的内角和判断出∠BAD=∠ADB=45°,根据等腰三角形的性质得出BD=AB=60;
(2)延长AE、DC交于点F,根据正方形的性质得出AF=BD=DF=60,然后在Rt△AFC中,利用锐角三角函数的定义得出CF的长,从而得出CD的长。
【考点精析】关于本题考查的平行线的性质和等腰三角形的性质,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副直角三角尺(即直角三角形AOB和直角三角形COD)的直角顶点O的重合,其中,在△AOB中,∠A=60°,∠B=30°,∠AOB=90°;在△COD中,∠C=∠D=45°,∠COD=90°.
(1)如图1,当OA在∠COD的外部,且∠AOC=45°时,①试说明CO平分∠AOB; ②试说明OA∥CD(要求书写过程);
(2)如图2,绕点O旋转直角三角尺AOB,使OA在∠COD的内部,且CD∥OB,试探索∠AOC=45°是否成立,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在RtABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为_______________

-
科目: 来源: 题型:
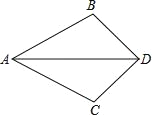
查看答案和解析>>【题目】如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件________;
(2)根据“ASA”需添加条件________;
(3)根据“AAS”需添加条件________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对全校学生进行文明礼仪知识测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)在扇形统计图中,表示“不合格”的扇形的圆心角度数为_________;
(3)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有________人达标.

相关试题

