Question

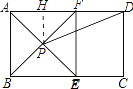
【题目】如图，在矩形ABCD中，AE平分∠BAD，交BC于E，过E做EF⊥AD于F，连接BF交AE于P，连接PD．

（1）求证：四边形ABEF是正方形；

（2）如果AB=6，AD=8，求tan∠ADP的值．

Answer 1

【答案】（1）证明见解析（2）

【解析】试题分析：（1）由矩形的性质得出∠FAB=∠ABE=90°，AF∥BE，证出四边形ABEF是矩形，再证明AB=BE，即可得出四边形ABEF是正方形；

（2）由正方形的性质得出BP=PF，BA⊥AD，∠PAF=45°，得出AB∥PH，求出DH=AD-AH=5，在Rt△PHD中，由三角函数即可得出结果．

试题解析：

（1）证明：∵四边形ABCD是矩形，

∴∠FAB=∠ABE=90°，AF∥BE，

∵EF⊥AD，

∴∠FAB=∠ABE=∠AFE=90°，

∴四边形ABEF是矩形，

∵AE平分∠BAD，AF∥BE，

∴∠FAE=∠BAE=∠AEB，

∴AB=BE，

∴四边形ABEF是正方形；

（2）解：过点P作PH⊥AD于H，如图所示：

∵四边形ABEF是正方形，

∴BP=PF，BA⊥AD，∠PAF=45°，

∴AB∥PH，

∵AB=6，

∴AH=PH=3，

∵AD=8，

∴DH=AD﹣AH=8﹣3=5，

在Rt△PHD中，∠PHD=90°．

∴tan∠ADP= = ．