【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,其中点B的坐标为(1,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是_____.

参考答案:
【答案】﹣1<k<![]()
【解析】分析:根据∠AOB=45°求出直线OA的解析式,然后与抛物线解析式联立求出有一个公共点时的k值,即为一个交点时的最大值,再求出抛物线经过点B时的k的值,即为一个交点时的最小值,然后写出k的取值范围即可.
详解:由图可知,∠AOB=45°,
∴直线OA的解析式为y=x,
联立![]() ,
,
消掉y得:x2-x+k=0,
△=b2-4ac=(-1)2-4×1×k=0,
即k=![]() 时,抛物线与OA有一个交点,
时,抛物线与OA有一个交点,
∵点B的坐标为(1,0),
∴OA=1,
∴点A的坐标为(![]() ,
,![]() ),
),
∴交点在线段AO上;
当抛物线经过点B(1,0)时,1+k=0,
解得k=-1,
∴要使抛物线y=x2+k与扇形OAB的边界总有两个公共点,实数k的取值范围是-1<k<![]() ,
,
故答案为:-1<k<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.

(1)求证:四边形ABEF是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )

A. 40°B. 45°C. 50°D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形
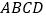 中,
中, ,
, ,
, ,且
,且 ,
,试求:(1)
 的度数;(2)四边形
的度数;(2)四边形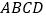 的面积(结果保留根号);
的面积(结果保留根号);
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为
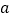 和
和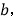 斜边长为
斜边长为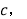 图(2)是以
图(2)是以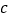 为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.
为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.(1)在图(3)处画出拼成的这个图形的示意图;
(2)利用(1)画出的图形证明勾股定理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=4cm,BC=6cm,∠B=60°,G是CD的中点,E是边AD上的动点(E不与A、D重合),且点E由A向D运动,速度为1cm/s,EG的延长线与BC的延长线交于点F,连接CE、DF,设点E的运动时间为
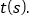
(1)求证:无论
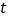 为何值,四边形CEDF都是平行四边形;
为何值,四边形CEDF都是平行四边形;(2)①当
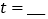 s时,CE⊥AD;
s时,CE⊥AD;②当
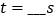 时,平行四边形CEDF的两条邻边相等.
时,平行四边形CEDF的两条邻边相等.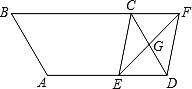
相关试题

