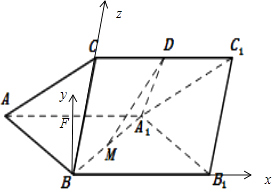
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面ABB1A1为菱形且 ![]() ,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1.
,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1. 
(Ⅰ)证明:直线MD∥平面ABC;
(Ⅱ)求二面角B﹣AC﹣A1的余弦值.
参考答案:
【答案】解:∵A1D⊥CC1 , 且D为中点,AA1=A1D=2,∴ ![]() , 又 BC=1,AB=BA1=2,∴CB⊥BA,CB⊥BA1 ,
, 又 BC=1,AB=BA1=2,∴CB⊥BA,CB⊥BA1 ,
又 BA∩BA1=B,∴CB⊥平面ABB1A1 ,
取AA1中点F,则BF⊥AA1 , 即BC,BF,BB1两两互相垂直,
以B为原点,BB1 , BF,BC分别为x,y,z轴,建立空间直角坐标系如图所示,B1(2,0,0),C(0,0,1), ![]() ,
, ![]() ,C1(2,0,1),D(1,0,1),
,C1(2,0,1),D(1,0,1), 
(I) 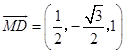 ,设平面ABC的法向量为
,设平面ABC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 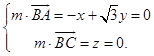 ,取
,取 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
又MD平面ABC,∴直线MD∥平面ABC.
(II) 设平面ACA1的法向量为n=(x1 , y1 , z1), ![]() ,
,
则 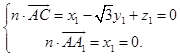 ,取
,取 ![]() ,
,
又由(Ⅰ)知平面ABC的法向量为 ![]() ,
,
设二面角B﹣AC﹣A1为θ,
∴ 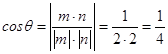 ,
,
∴二面角B﹣AC﹣A1的余弦值为 ![]()
【解析】由已知可得 ![]() ,CB⊥平面ABB1A1 , 取AA1中点F可得BC,BF,BB1两两互相垂直 以B为原点,BB1 , BF,BC分别为x,y,z轴,建立空间直角坐标系,B1(2,0,0),C(0,0,1),
,CB⊥平面ABB1A1 , 取AA1中点F可得BC,BF,BB1两两互相垂直 以B为原点,BB1 , BF,BC分别为x,y,z轴,建立空间直角坐标系,B1(2,0,0),C(0,0,1), ![]() ,
, ![]() ,C1(2,0,1),D(1,0,1),
,C1(2,0,1),D(1,0,1), ![]() ,利用空间向量求解.
,利用空间向量求解.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,D为线段BC的中点,AB=2AC=2,tan∠CAD=sin∠BAC,则BC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,a1=1,an+1=(n+1)an+(n+1)!. (Ⅰ)求证:数列
 是等差数列,并求{an}的通项公式;
是等差数列,并求{an}的通项公式;
(Ⅱ)求{an}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂的污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为p(0<p<1).经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放. 某厂现有4个标准水量的A级水池,分别取样、检测.多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
现有以下四种方案,
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:混在一起化验.
化验次数的期望值越小,则方案的越“优”.
(Ⅰ) 若 ,求2个A级水样本混合化验结果不达标的概率;
,求2个A级水样本混合化验结果不达标的概率;
(Ⅱ) 若 ,现有4个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
,现有4个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
(Ⅲ) 若“方案三”比“方案四”更“优”,求p的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆M:(x﹣a)2+(y﹣b)2=9,M在抛物线C:x2=2py(p>0)上,圆M过原点且与C的准线相切. (Ⅰ)求C的方程;
(Ⅱ)点Q(0,﹣t)(t>0),点P(与Q不重合)在直线l:y=﹣t上运动,过点P作C的两条切线,切点分别为A,B.求证:∠AQO=∠BQO(其中O为坐标原点). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣x,g(x)=ex﹣ax﹣1(e为自然对数的底数).
(1)讨论函数g(x)的单调性;
(2)当x>0时,f(x)≤g(x)恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1:ρ2﹣4ρcosθ+3=0,θ∈[0,2π],曲线C2:ρ=
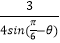 ,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
,θ∈[0,2π]. (Ⅰ)求曲线C1的一个参数方程;
(Ⅱ)若曲线C1和曲线C2相交于A、B两点,求|AB|的值.
相关试题

