【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
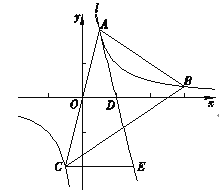
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
参考答案:
【答案】(1)m=1;y=-4x+4;(2)E(![]() ,-2);(3)证明见解析.
,-2);(3)证明见解析.
【解析】试题分析:(1)将点A(![]() ,2)代入
,2)代入![]() 求出m的值,再将A(
求出m的值,再将A(![]() ,2),D(1,0)分别代入y=kx+b,求出k、b的值;
,2),D(1,0)分别代入y=kx+b,求出k、b的值;
(2)由反比例函数图象的中心对称性可知点C的坐标为C(﹣![]() ,﹣2),由yE=yC求出E点坐标.
,﹣2),由yE=yC求出E点坐标.
(3)作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,由于点B(3,n)在反比例函数图象上,求出n=![]() ,在Rt△ABG中、Rt△BCH中,求出tan∠ABH和tan∠CBH的值即可.
,在Rt△ABG中、Rt△BCH中,求出tan∠ABH和tan∠CBH的值即可.
试题解析:解:(1)∵点A(![]() ,2)在反比例函数
,2)在反比例函数![]() (m为常数)的图象上,∴m=
(m为常数)的图象上,∴m=![]() ×2=1,∴反比例函数
×2=1,∴反比例函数![]() (m为常数)对应的函数表达式是
(m为常数)对应的函数表达式是![]() .
.
设直线l对应的函数表达式为y=kx+b(k,b为常数,k≠0).
∵直线l经过点A(![]() ,2),D(1,0),∴
,2),D(1,0),∴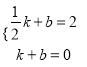 ,解得:
,解得: ![]() ,∴直线l对应的函数表达式为y=﹣4x+4.
,∴直线l对应的函数表达式为y=﹣4x+4.
(2)由反比例函数图象的中心对称性可知点C的坐标为C(﹣![]() ,﹣2).
,﹣2).
∵CE∥x轴交直线l于点E,∴yE=yC,∴点E的坐标为E(![]() ,﹣2).
,﹣2).
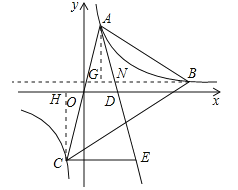
(3)如图,作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,∵点B(3,n)在反比例函数图象上,∴n=![]() ,∴B(3,
,∴B(3, ![]() ),G(
),G(![]() ,
, ![]() ),H(﹣
),H(﹣![]() ,
, ![]() ).
).
在Rt△ABG中,tan∠ABH= ,在Rt△BCH中,tan∠CBH=
,在Rt△BCH中,tan∠CBH= ,∴tan∠ABN=tan∠CBN.
,∴tan∠ABN=tan∠CBN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
(1)求证:△CDE≌△CBF;
(2)当DE=
 时,求CG的长;
时,求CG的长;(3)连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方形分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;
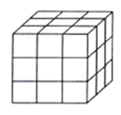
(1)只有一面涂有颜色的概率;
(2)至少有两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学学习中,及时对知识进行归纳和整理是完善知识结构的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:

(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ .
(2)如果点C的坐标为(1,3) ,求不等式
 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:

(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有A,B,C三种款式的帽子,E,F二种款式的围巾,穿戴时小婷任意选一顶帽子和一条围巾.
(1)用合适的方法表示搭配的所有可能性结果.
(2)求小婷恰好选中她所喜欢的A款帽子和E款围巾的概率.
相关试题

