【题目】如图,在△ABC中,点D为BC边的中点,点E为AC上一点,将∠C沿DE翻折,使点C落在AB上的点F处,若∠AEF=50°,则∠A的度数为____.

参考答案:
【答案】65°
【解析】
由点D为BC的中点,得BD=CD,根据折叠的性质得到DF=CD,∠EFD=∠C,得DF=BD,根据等腰三角形的性质得∠BFD=∠B,由三角形的内角和与平角的定义得∠A=∠AFE,于是求出∠A的度数.
∵点D为BC的中点,
∴BD=CD,
∵将∠C沿DE翻折,使点C落在AB上的点F处,
∴DF=CD,∠EFD=∠C,
∴DF=BD,
∴∠BFD=∠B,
∵∠A=180°-∠C-∠B,∠AFE=180°-∠EFD-∠DFB,
∴∠A=∠AFE,
∵∠AEF=50°,
∴∠A=![]() (180°-50°)=65°.
(180°-50°)=65°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图
 ,在
,在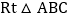 中,
中,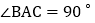 ,
,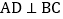 于点D.可知:
于点D.可知: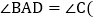 不需要证明
不需要证明 ;
;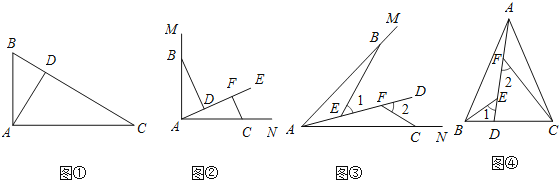
 特例探究:如图
特例探究:如图 ,
, ,射线AE在这个角的内部,点B、C在
,射线AE在这个角的内部,点B、C在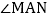 的边AM、AN上,且
的边AM、AN上,且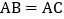 ,
,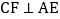 于点F,
于点F,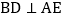 于点
于点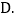 证明:
证明: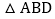 ≌
≌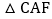 ;
; 归纳证明:如图
归纳证明:如图 ,点B,C在
,点B,C在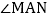 的边AM、AN上,点E,F在
的边AM、AN上,点E,F在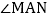 内部的射线AD上,
内部的射线AD上,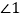 、
、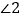 分别是
分别是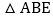 、
、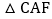 的外角
的外角 已知
已知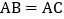 ,
,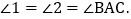 求证:
求证: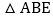 ≌
≌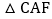 ;
; 拓展应用:如图
拓展应用:如图 ,在
,在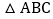 中,
中,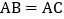 ,
, 点D在边BC上,
点D在边BC上,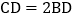 ,点E、F在线段AD上,
,点E、F在线段AD上,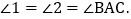 若
若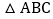 的面积为24,则
的面积为24,则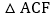 与
与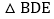 的面积之和为______
的面积之和为______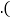 直接写出结果
直接写出结果
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
①∠ABN=60°;②AM=1;③QN= ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是  .
.
其中正确结论的序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则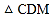 周长的最小值为
周长的最小值为


A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
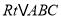 中,
中,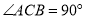 ,点
,点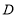 在
在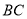 的延长线上,
的延长线上,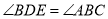 ,
,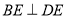 于
于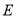 ,
,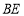 交于点
交于点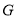 .
.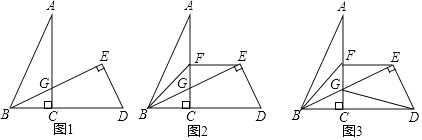
(1)如图1,请写出
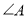 与
与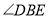 的数量关系;
的数量关系;(2)如图2,若
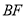 平分
平分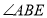 ,
,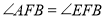 ,求证:
,求证: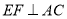 ;
;(3)在(2)的条件下,如图3,连接
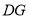 ,若
,若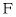 是
是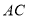 中点,
中点,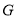 是
是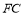 中点,
中点,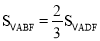 ,
,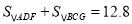 ,
,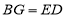 ,求
,求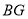 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为解决“最后一公里”的交通接驳问题,某市投放了大量公租自行车使用,到2014年底,全市已有公租自行车25000辆,租赁点600个,预计到2016年底,全市将有公租自行车50000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
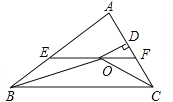
①EF=BE+CF;
②∠BOC=90°+
 ∠A;
∠A;③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则
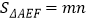 .
.其中正确的结论是____.(填序号)
相关试题

