Question

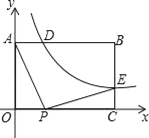
【题目】如图，已知矩形OABC中，OA=3，AB=4，双曲线y=（k＞0）与矩形两边AB、BC分别交于D、E，且BD=2AD

（1）求k的值和点E的坐标；

（2）点P是线段OC上的一个动点，是否存在点P，使∠APE=90°？若存在，求出此时点P的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）k="4," E（4，1）；（2）存在要求的点P，坐标为（1，0）或（3，0）．

【解析】试题分析：（1）由矩形ABCD中，AB=4，BD=2AD，可得3AD=4，即可求得 AD的长，然后求得点D的坐标，即可求得K的值，继而求得点 E的坐标；（2）首先假设存在要求的点P坐标为（m,0），OP=m,CP=4-m,由∠APE=90，易证得△AOP∽△PCE，然后由相似三角形的对应边成比例，求得m的值，继而求得此时点P的坐标．

试题解析：（9分）（1）∵AB=4，BD=2AD，∴AB=AD+BD=AD+2AD=3AD=4，∴AD=，

又∵OA=3，所以D（，3），∵点D在双曲线上，所以k=×3=4．

∵四边形OABC为矩形,∴AB=OC=4，∴点E的横坐标为4．

把x=4代入中，得y=1，所以E（4，1）．

（2）假设存在要求的点P坐标为（m，0），OP=m，CP=4-m．

∵∠APE=90，∴∠APO+∠EPC=90,又∵∠APO+∠OAP=90, ∴∠EPC=∠OAP，

又∵∠AOP=∠PCE=90，∴△AOP∽△PCE，∴，

∴,解得：m=1或m=3．

所以，存在要求的点P，坐标为（1，0）或（3，0）．