【题目】在平面直角坐标系xOy中,给出如下定义:
对于⊙C及⊙C外一点P,M,N是⊙C上两点,当∠MPN最大,称∠MPN为点P关于⊙C的“视角”.直线l与⊙C相离,点Q在直线l上运动,当点Q关于⊙C的“视角”最大时,则称这个最大的“视角”为直线l关于⊙C的“视角”.
(1)如图,⊙O的半径为1,
①已知点A(1,1),直接写出点A关于⊙O的“视角”;已知直线y = 2,直接写出直线y = 2关于⊙O的“视角”;
②若点B关于⊙O的“视角”为60°,直接写出一个符合条件的B点坐标;
(2)⊙C的半径为1,
①C的坐标为(1,2),直线l: y=kx + b(k > 0)经过点D(![]() ,0),若直线l关于⊙C的“视角”为60°,求k的值;
,0),若直线l关于⊙C的“视角”为60°,求k的值;
②圆心C在x轴正半轴上运动,若直线y =![]() x +
x +![]() 关于⊙C的“视角”大于120°,直接写出圆心C的横坐标xC的取值范围.
关于⊙C的“视角”大于120°,直接写出圆心C的横坐标xC的取值范围.

参考答案:
【答案】(1)① 90,60;②本题答案不唯一,如:B (0,2);(3)![]() .
.
【解析】试题分析:
(1)由题意可知,点P关于⊙O的“视角”是指从点P引出两条射线,当两条射线和⊙O相切时,两条射线所形成的的夹角就是点P关于⊙O的“视角”;直线![]() 关于⊙O的“视角”是指当直线
关于⊙O的“视角”是指当直线![]() 与⊙O相离时,直线
与⊙O相离时,直线![]() 上的点Q距离圆心O最近时,点Q关于⊙O的“视角”就是直线
上的点Q距离圆心O最近时,点Q关于⊙O的“视角”就是直线![]() 关于⊙O的“视角”;由此可根据已知条件解答第一问;
关于⊙O的“视角”;由此可根据已知条件解答第一问;
(2)①由题意可知,若直线l关于⊙C的“视角”为60°,则说明在直线![]() 上存在一点P距离点C最近,且点P关于⊙C的“视角”为60°,则此时点P是
上存在一点P距离点C最近,且点P关于⊙C的“视角”为60°,则此时点P是![]() 与以点C为圆心,2为半径的圆相切的切点,如图1,过点C作CH⊥
与以点C为圆心,2为半径的圆相切的切点,如图1,过点C作CH⊥![]() 轴于点H,PE⊥
轴于点H,PE⊥![]() 轴于点E,由已知分析可得DP=DH=
轴于点E,由已知分析可得DP=DH=![]() ,∠PDE=60°,在△PDE中可求得DE和PE的长,得到点P的坐标,把P、D的坐标代入直线
,∠PDE=60°,在△PDE中可求得DE和PE的长,得到点P的坐标,把P、D的坐标代入直线![]() 的解析式可求得k的值;
的解析式可求得k的值;
②如图2,由已知易得直线![]() 与
与![]() 轴相交于点A(-1,0),与
轴相交于点A(-1,0),与![]() 轴相交于点B(0,
轴相交于点B(0, ![]() ),若此时直线
),若此时直线![]() 关于⊙C的视角∠EPF=120°,由已知条件求得OC的长,可得点C的坐标;如图3,当沿着
关于⊙C的视角∠EPF=120°,由已知条件求得OC的长,可得点C的坐标;如图3,当沿着![]() 轴向左移动时,直线
轴向左移动时,直线![]() 关于⊙C的视角会变大,当直线
关于⊙C的视角会变大,当直线![]() 和⊙C相切于点P时,由已知条件可求得OC的长,可得此时点C的坐标;综合起来可得
和⊙C相切于点P时,由已知条件可求得OC的长,可得此时点C的坐标;综合起来可得![]() 的取值范围.
的取值范围.
试题解析:
(1)①如下图,当点A的坐标为(1,1)时,易得点A关于⊙O的视角为90°;
∵直线y=2上距离圆心O最近的点是直线y=2与y轴的交点P,过点P作⊙O的两条切线PC、PD,切点为C、D,则直线y=2关于⊙O的视角是∠CPD,连接OD,由已知条件可求得∠OPD=30°,∴∠CPD=60°,即直线y=2关于⊙O的视角为60°.
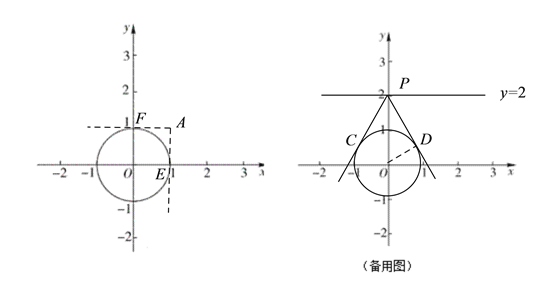
②由①中第2小问可知,满足条件的点B在以O为圆心,2为半径的圆上,这样的点很多,比如说点B(0,2).
(2)①∵直线l: y=kx + b(k > 0)经过点D(![]() ,0),
,0),
∴![]() .
.
∴![]() .
.
∴直线l: ![]() .
.
设点P在直线![]() 上,若点P关于⊙C的“视角”为60°,则点P在以C为圆心,2为半径的圆上.
上,若点P关于⊙C的“视角”为60°,则点P在以C为圆心,2为半径的圆上.
∵直线l关于⊙C的 “视角”为60°,
∴此时,点P是直线l上与圆心C的距离最短的点.
∴CP⊥直线l.
即直线l是以C为圆心,2为半径的圆的一条切线,如图1所示.
作过点C作CH⊥![]() 轴于点H,PE⊥
轴于点H,PE⊥![]() 轴于点E,
轴于点E,
∴点H的坐标为(1,0),
又∵点D的坐标为![]() ,
,
∴DH =![]() =PD.
=PD.
∴tan∠CDH=![]() ,
,
∴∠CDH=30°,∠PDH=60°,
∴DE=PD![]() cos60°=
cos60°=![]() ,PE= PD
,PE= PD![]() sin60°=3,
sin60°=3,
∴OE=DH-DE-OH=![]() ,
,
∴点P的坐标(![]() ,3).
,3).
把点P的坐标代入l: ![]() ,解得: k=
,解得: k=![]() .
.
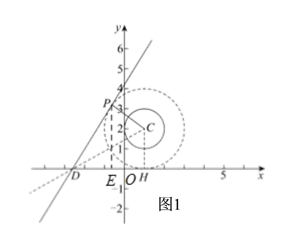
②如图2,由已知易得直线![]() 与
与![]() 轴相交于点A(-1,0),与
轴相交于点A(-1,0),与![]() 轴相交于点B(0,
轴相交于点B(0, ![]() ),
),
若此时直线![]() 关于⊙C的视角∠EPF=120°,
关于⊙C的视角∠EPF=120°,
则∠EPC=60°,∠PEC=90°,CE=1,∴∠PCE=30°,
∴PC=![]() ,AC=
,AC=![]() ,
,
∴OC=AC-OA=![]() ,
,
∴此时![]() =
=![]() ;
;
如图3,当沿着![]() 轴向左移动时,直线
轴向左移动时,直线![]() 关于⊙C的视角会变大,当直线
关于⊙C的视角会变大,当直线![]() 和⊙C相切于点P时,连接CP,
和⊙C相切于点P时,连接CP,
∵在△ABO中,AO=1,BO=![]() ,
,
∴tan∠BAO=![]() ,
,
∴∠BAO=60°,
∴AC=![]() ,
,
∴OC=AC-OA=![]() ,
,
∴此时![]() =
=![]() ,
,
综上所述, ![]() 的取值范围为:
的取值范围为: ![]() .
.
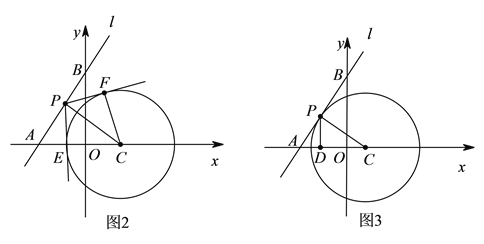
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
(1)求证:AC是⊙O的切线;
(2)若
 ,BD=5,求BF的长.
,BD=5,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王在静水中划船每小时速度12Km,今往返于某河,逆流时用了10h,顺流时用了6h,求此河的水流速度
-
科目: 来源: 题型:
查看答案和解析>>【题目】钟表在3点30分时,它的时针和分针所成的角是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
(1)在由原方程得到方程①的过程中,利用 法(把未知数x换为 y)达到降次的目的.
(2)解方程:(x2+3x)2+5(x2+3x)-6=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年,6月12日为端午节,在端午节前夕三位同学到某超市调研一种进价为2元的粽子的售销情况,请跟据小丽提供的信息,解答小华和小明提出的问题。
小丽:每个定价3元,每天能卖出500个,而且,这种粽子每上涨0.1元,其售销量 将减小10个。
小华:照你所说,如果实现每天不低于800元的售销利润,那么定价应在什么范围 内?莫忘了物价局规定售价不能超过进价的240%哟。
小明:该如何定价,才会使每天的利润最大?最大利润是多少?
(1)请回答小华的问题。
(2)请回答小明的问题。
相关试题

