【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).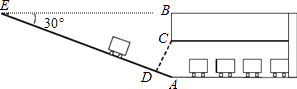
参考答案:
【答案】解:由题意得,AB⊥EB,CD⊥AE,
∴∠CDA=∠EBA=90°,
∵∠E=30°,
∴AB= ![]() AE=8米,
AE=8米,
∵BC=1.2米,
∴AC=AB﹣BC=6.8米,
∵∠DCA=90°﹣∠A=30°,
∴CD=AC×cos∠DCA=6.8× ![]() ≈5.9米.
≈5.9米.
答:该校地下停车场的高度AC为6.8米,限高CD约为5.9米.
【解析】根据题意和正弦的定义求出AB的长,根据余弦的定义求出CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
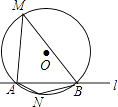
A.2
B.4
C.4
D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
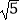 cm,且tan∠EFC=0.75,则矩形ABCD的周长为 .
cm,且tan∠EFC=0.75,则矩形ABCD的周长为 . 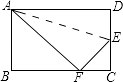
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,﹣1),E(﹣1,﹣7).
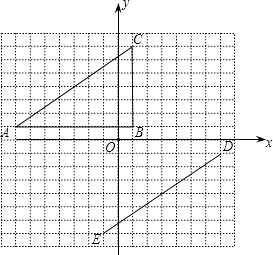
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算.
①
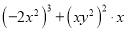 ②
②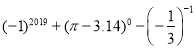
③
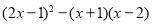 ④
④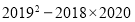
(2)先化简,再求值.
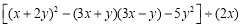 ,其中
,其中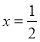 ,
,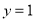 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( ).
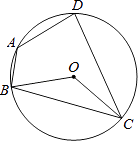
A.120°
B.130°
C.140°
D.150° -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
如图,已知
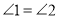 ,
,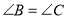 ,可推得
,可推得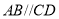 .
.理由如下:∵
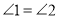 (已知),
(已知),且
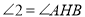 ( )
( )∴
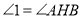 (等量代换)
(等量代换)∴________∥________( )
∴∠________
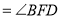 ( )
( )又∵
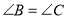 (已知)
(已知)∴
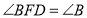 ( )
( )∴
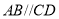 ( )
( )
相关试题

