【题目】如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=10,则∠ABC= , 对角线AC的长为 . 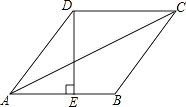
参考答案:
【答案】120°;10 ![]()
【解析】解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AD∥BC,
∵E是AB的中点,且DE⊥AB,
∴AE= ![]() AD,
AD,
∴sin∠ADE= ![]() ,
,
∴∠ADE=30°,
∴∠DAE=60°,
∵AD∥BC,
∴∠ABC=180°﹣60°=120°;
连接BD,交AC于点O,
在菱形ABCD中,∠DAE=60°,
∴∠CAE=30°,AB=10,
∴OB=5,
根据勾股定理可得:AO= ![]() =5
=5 ![]() ,
,
即AC=10 ![]() .
.
所以答案是:120°;10 ![]() .
.
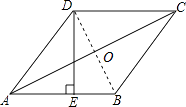
【考点精析】本题主要考查了线段垂直平分线的性质和菱形的性质的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
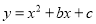 (
(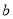 ,
, 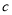 为常数).
为常数).(1)当
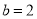 ,
, 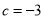 时,求二次函数的最小值;
时,求二次函数的最小值;(2)当
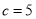 时,若在函数值
时,若在函数值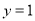 的情况下,只有一个自变量
的情况下,只有一个自变量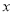 的值与其对应,求此时二次函数的解析式;
的值与其对应,求此时二次函数的解析式;(3)当
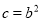 时,若在自变量
时,若在自变量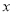 的值满足
的值满足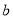 ≤
≤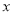 ≤
≤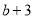 的情况下,与其对应的函数值
的情况下,与其对应的函数值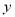 的最小值为21,求此时二次函数的解析式.
的最小值为21,求此时二次函数的解析式. -
科目: 来源: 题型:
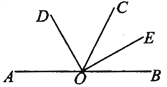
查看答案和解析>>【题目】如图,已知A、O、B三点在一直线上,∠AOC=120°,OD、OE分别是∠AOC,
∠BOC的平分线.
(1)判断OD与OE的位置关系;
(2)当∠AOC大小发生变化时,OD、OE仍分别是∠AOC、∠BOC的平分线,则OD与OE的位置关系是否改变? 请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣3x=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,请你在表盘上画出时针与分针,使时针与分针恰好互相垂直.
(1) 时针和分针互相垂直的整点时刻分别为________ ;
(2)一天24小时,时针与分针互相垂直________次.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx-3(a≠0)的图象经过点(1,3),则代数式1-a-b的值为____.
相关试题

