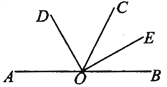
【题目】如图,已知A、O、B三点在一直线上,∠AOC=120°,OD、OE分别是∠AOC,
∠BOC的平分线.
(1)判断OD与OE的位置关系;
(2)当∠AOC大小发生变化时,OD、OE仍分别是∠AOC、∠BOC的平分线,则OD与OE的位置关系是否改变? 请说明理由.
参考答案:
【答案】(1)垂直;(2)不变,理由见解析.
【解析】试题分析:(1)OD⊥OE,由∠AOC=120°,可得∠BOC=60°,再根据角平分线的定义可得∠DOC=60°,∠EOC=30°,从而得∠DOE=90°,即OD⊥OE;
(2)不变, 由角平分线的定义可得∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠COB,从而得∠DOE=90°,从而可得OD与OE的位置关系不发生改变.
∠COB,从而得∠DOE=90°,从而可得OD与OE的位置关系不发生改变.
试题解析:(1)OD⊥OE,理由如下:
∵∠AOC=120°,∴∠BOC=60°,
∵OD是∠AOC的平分线,OE是∠BOC的平分线,
∴∠DOC=60°,∠EOC=30°,
∴∠DOE=60°+30°=90°,
即OD⊥OE;
(2)不变,理由如下:
∵OD,OE分别是∠AOC,∠BOC的平分线,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠COB,
∠COB,
∴∠DOE=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)=![]() ×180°=90°,
×180°=90°,
∴OD⊥OE,
即OD与OE的位置关系不发生改变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某多边形的内角和是其外角和的3倍,则此多边形的边数是( )
A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的边长为2,每个外角都为60°,则这个多边形的周长是( )
A. 8 B. 12 C. 16 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
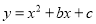 (
(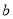 ,
, 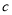 为常数).
为常数).(1)当
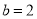 ,
, 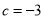 时,求二次函数的最小值;
时,求二次函数的最小值;(2)当
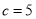 时,若在函数值
时,若在函数值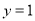 的情况下,只有一个自变量
的情况下,只有一个自变量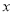 的值与其对应,求此时二次函数的解析式;
的值与其对应,求此时二次函数的解析式;(3)当
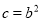 时,若在自变量
时,若在自变量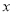 的值满足
的值满足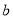 ≤
≤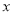 ≤
≤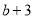 的情况下,与其对应的函数值
的情况下,与其对应的函数值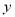 的最小值为21,求此时二次函数的解析式.
的最小值为21,求此时二次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣3x=
-
科目: 来源: 题型:
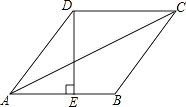
查看答案和解析>>【题目】如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=10,则∠ABC= , 对角线AC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,请你在表盘上画出时针与分针,使时针与分针恰好互相垂直.
(1) 时针和分针互相垂直的整点时刻分别为________ ;
(2)一天24小时,时针与分针互相垂直________次.

相关试题

