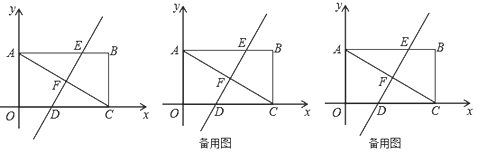
【题目】如图,平面直角坐标系中,矩形![]() 的对角线
的对角线![]() ,
,![]() .
.
(1)把矩形![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与
分别与![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(2)若点![]() 在直线
在直线![]() 上,平面内是否存在点
上,平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)存在;N点坐标为:
;(2)存在;N点坐标为:![]() ,
,![]() ,
,![]() .
.
【解析】
(1)由含30度直角三角形性质,得OA=![]() AC=12,然后求出OC,然后求得直线AC的解析式,由折叠知DE⊥AC,点F是AC中点,然后可以求得DE的解析式;
AC=12,然后求出OC,然后求得直线AC的解析式,由折叠知DE⊥AC,点F是AC中点,然后可以求得DE的解析式;
(2)分为①以OF,FM为边;②以FM为边,OF为对角线;③以OF为边,FM为对角线,三类进行讨论分析,然后可求N点坐标.
解:(1)根据题意,在直角三角形AOC中,∠AOC=90°,![]() ,
,![]() ,
,
∴![]() ,即点A为:(0,12),
,即点A为:(0,12),
由勾股定理,得![]() ,即点C为:(
,即点C为:(![]() ),
),
设直线AC的方程为![]() ,把A、C坐标代入,得
,把A、C坐标代入,得
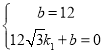 ,解得:
,解得: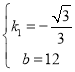 ,
,
∴直线AC的方程为:![]() ,
,
根据折叠的性质,有DE⊥AC,点F是AC中点,
∴直线DE的斜率为:![]() ,点F为(
,点F为(![]() ),
),
则设直线DE的解析式为![]() ,把点F代入,得
,把点F代入,得
![]() ,解得:
,解得:![]() ,
,
∴直线DE的解析式为:![]() ;
;
(2)存在;
①以OF,FM为边,如图
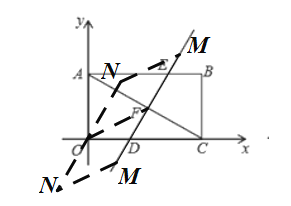
由(1)知,直线DE的解析式为:![]() ,
,
令![]() ,则
,则![]() ,
,
∴点D坐标为:![]() ,
,
∵ONMF是菱形
∴OF=ON,ON∥DE
∴直线ON的解析式为:![]() ,
,
设N点坐标为:(![]() ),
),
∴![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴N点坐标为:![]() ;
;
②以FM为边,OF为对角线;连接AD,CE,如图:
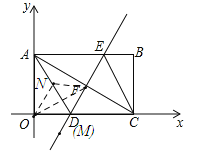
由折叠知,四边形ADCE是菱形,
∴AD=CD=![]() ,
,
∴∠DAC=∠DCA=30°,
∴∠OAD=30°,
∴∠OAD=∠DAC,AD=AD,∠AOD=∠AFD=90°,
∴△AOD≌△AFD,
∴AO=AF,OD=FD,
∴AD是OF 的垂直平分线,
∵四边形ONFM是菱形,
∴MN是OF的垂直平分线,
∴M与D重合,即M为![]() ,
,
设N为![]() ,
,
∵OF与MN互相平分,
∴![]() ,
,![]() ,
,
解得:![]() ,
,
∴N点坐标为:![]() ;
;
③以OF为边,FM为对角线,如图:
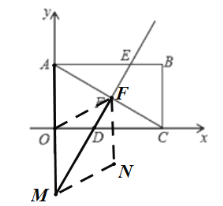
∵直线DE的解析式为:![]() ,
,
∴直线DE与y轴的交点为(0,-12),
∵四边形OFNM是菱形,![]() ,
,
∴OM=OF=12,
∴点M的坐标为(0,-12),
∵OM∥FN,OM=FN=12,且点F为(![]() ),
),
∴N点坐标为:![]() ;
;
综合上述,N点坐标为:![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
(1)若他早上领取备用金4000元,那么下班时应交回银行_________元钱.
(2)请判断在这七次办理业务中,小张在第_______次业务办理后手中现金最多,第_________次业务办理后手中现金最少.
(3)若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
(4)若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.
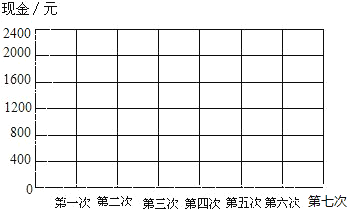
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ ABCD中,E是AD边上一点,AD=4
 ,CD=3,ED=
,CD=3,ED= ,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将
,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将  CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.
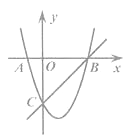
(1)求直线BC的函数关系式;
(2)当y1>y2时,请直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知AB是⊙O 的直径,C是⊙O 上一点,∠ACB的平分线交⊙O 于点D,作PD∥AB,交CA的延长线于点P.连结AD,BD.
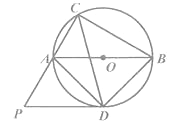
求证:(1)PD是⊙O 的切线;
(2)△PAD
 △DBC.
△DBC. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=
 x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
A. (-3,0) B. (-6,0) C. (-
 ,0) D. (-
,0) D. (- ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】填空并解答相关问题:
(1)观察下列数1,3,9,27,81…,发现从第二项开始,每一项除以前一项的结果是一个常数,这个常数是________;根据此规律,如果an (n为正整数)表示这列数的第n项,那么an =__________;
你能求出它们的和吗?
计算方法:如果要求1+3+32+33+…+320的值,
可令S=1+3+32+33+…+320①
将①式两边同乘以3,得3S=3+32+33+…+320+321②
由②式左右两边分别减去①式左右两边,
得3S-S=(3+32+33+…+320+321)-(1+3+32+33+…+320),
即2S=321-1,两边同时除以2得
 .
.(2)你能用类比的思想求1+6+62+63+…+6100的值吗?写出求解过程.
(3)你能用类比的思想求1+m+m2+m3+…+mn(其中mn≠0,m≠1)的值吗?写出求解过程.
相关试题

