【题目】如图,己知AB是⊙O 的直径,C是⊙O 上一点,∠ACB的平分线交⊙O 于点D,作PD∥AB,交CA的延长线于点P.连结AD,BD.
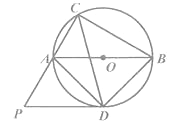
求证:(1)PD是⊙O 的切线;
(2)△PAD![]() △DBC.
△DBC.
参考答案:
【答案】见解析
【解析】(1)根据角平分线的定义得出∠1=∠3,得出弧AD=弧BD,根据垂径定理可得出OD⊥AB,再根据PD∥AB,就可证得OD⊥PD,即可得证;
(2)根据圆内接四边形的定理,可证得∠2=∠CBD,再根据圆周角定理及等腰直角三角形的性质,可证得∠ADP=∠1,然后根据相似三角形的判定定理,可证得结论.
(1)证明:如图,连接OD
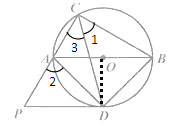
∵CD平分∠ACB
∴∠1=∠3
∴弧AD=弧BD
∴OD⊥AB
∵PD∥AB
∴OD⊥PD
∵OD是半径
∴PD是⊙O的切线
(2)证明:∵四边形ADBC是圆的内接四边形,
∴∠CAD+∠CBD=180°
∵∠2+∠CAD=180°
∴∠2=∠CBD
∵AB是圆的直径
∴∠ADO+∠BDO=90°,∠1+∠3=90°,即∠1=45°
∵弧AD=弧BD,OD⊥AB
∴AD=BD
∴∠ADO=45°
∵∠ADO+∠ADP=90°
∴∠ADP=45°=∠1
∴△PAD∽△DBC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ ABCD中,E是AD边上一点,AD=4
 ,CD=3,ED=
,CD=3,ED= ,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将
,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将  CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.
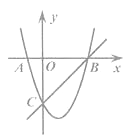
(1)求直线BC的函数关系式;
(2)当y1>y2时,请直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形
 的对角线
的对角线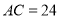 ,
,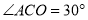 .
.(1)把矩形
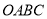 沿直线
沿直线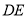 对折,使点
对折,使点 落在点
落在点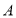 处,折痕
处,折痕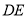 分别与
分别与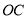 、
、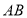 、
、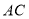 相交于点
相交于点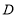 、
、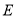 、
、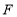 ,求直线
,求直线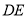 的解析式;
的解析式;(2)若点
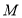 在直线
在直线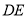 上,平面内是否存在点
上,平面内是否存在点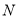 ,使以
,使以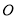 、
、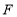 、
、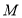 、
、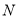 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=
 x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
A. (-3,0) B. (-6,0) C. (-
 ,0) D. (-
,0) D. (- ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】填空并解答相关问题:
(1)观察下列数1,3,9,27,81…,发现从第二项开始,每一项除以前一项的结果是一个常数,这个常数是________;根据此规律,如果an (n为正整数)表示这列数的第n项,那么an =__________;
你能求出它们的和吗?
计算方法:如果要求1+3+32+33+…+320的值,
可令S=1+3+32+33+…+320①
将①式两边同乘以3,得3S=3+32+33+…+320+321②
由②式左右两边分别减去①式左右两边,
得3S-S=(3+32+33+…+320+321)-(1+3+32+33+…+320),
即2S=321-1,两边同时除以2得
 .
.(2)你能用类比的思想求1+6+62+63+…+6100的值吗?写出求解过程.
(3)你能用类比的思想求1+m+m2+m3+…+mn(其中mn≠0,m≠1)的值吗?写出求解过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市共有一中、二中、三中等3所高中,有一天所有高二学生参加了一次数学测试,阅卷后老师们对第10题进行了分析,把每个学生的解答情况归结为下列四类情况之一:A(概念错误),B(计算错误),C(基本正确),D(完全正确).各校出现这四类情况的人数占本校高二学生数的百分比见下面的条形统计图:
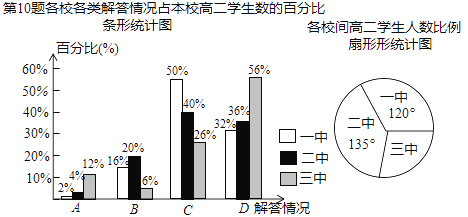
已知一中高二学生有400名,这三所学校之问高二学生人数的比例见扇形统计图.
(1)求全市高二学生总数;
(2)求全市解答完全正确的高二学生数占高二学生总数的百分比;
(3)请你对三中高二数学老师提一个值得关注的教学建议,并说明理由.
相关试题

