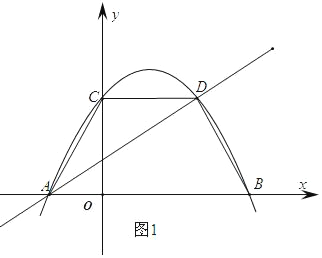
【题目】如图,平面直角坐标系中,直线l:y=![]() x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
(1)求点A的坐标;
(2)求此二次函数的解析式;
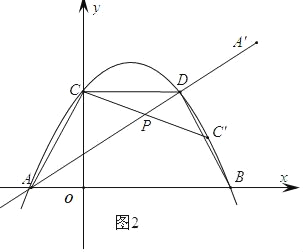
(3)点P为直线l上一动点,将线段AC绕点P顺时针旋转α°(0°<α°<360°)得到线段A'C'(点A,A'是对应点,点C,C'是对应点).请问:是否存在这样的点P,使得旋转后点A'和点C'分别落在直线l和抛物线y=ax2﹣3ax+c的图象上?若存在,请直接写出点A'的坐标;若不存在,请说明理由.
参考答案:
【答案】(1) A(﹣1,0);(2) y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2;(3)见解析.
x+2;(3)见解析.
【解析】
(1)由题意可得C(0,c),且CD∥x轴,可得D(3,c),根据面积比可得AB=5.由对称性可得点A(-2m,0)到对称轴的距离2倍是5,可求m,即可求A点坐标.
(2)由直线l过D点可求D(3,2),由A,B关于对称轴对称可求B(4,0),则可用交点式求二次函数的解析式.
(3)由点A是直线l上一点,绕直线l上点P旋转,且落在直线l上,因此可得点A与点A'重合,或点A绕点P旋转180°得到A'.设C'(a,-![]() a2+
a2+![]() a+2)根据中点坐标公式可求A'点坐标.
a+2)根据中点坐标公式可求A'点坐标.
解:(1)
∵二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点
∴C(0,c,),对称轴是直线x=![]() =
=![]() .
.
∵CD∥x轴.
∴C,D关于对称轴直线x=![]() 对称.
对称.
∴D(3,c).
∵S△ACD:S△ABD=3:5.且△ACD和△ABD是等高的.
∴![]() .
.
∴AB=5.
∵直线y=![]() x+m与x轴交于A点,
x+m与x轴交于A点,
∴A(﹣2m,0).
∵点A,点B关于对称轴x=![]() 对称.
对称.
∴2×[![]() ﹣(﹣2m)]=5.
﹣(﹣2m)]=5.
∴m=![]() .
.
∴A(﹣1,0),且AB=5.
∴B(4,0).
(2)设抛物线解析式y=a(x+1)(x﹣4).
∵m=![]() .
.
∴直线AD解析式y=![]() x+
x+![]() .
.
∵D(3,c)在直线AD上.
∴c=![]() +
+![]() =2.
=2.
∴D(3,2)且在抛物线上.
∴2=a(3+1)(3﹣4).
∴a=﹣![]() .
.
∴抛物线解析式y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2.
x+2.
(3)∵点A在直线l上,旋转后A'点落在直线l上,
∴点A与点A'重合,或者点A绕着点P旋转180°.
当点A与点A'重合时,A'(﹣1,0).
当点A绕着点P旋转180°得到A',点C绕着点P旋转180°得到C'
∴AP=A'P,CP=CP'.
如图2:
设C'(a,﹣![]() a2+
a2+![]() a+2).
a+2).
∵C( 0,2),CP=CP'.
∴P(![]() a,﹣
a,﹣![]() a2+
a2+![]() a+2).
a+2).
∵点P在直线l上,
∴﹣![]() a2+
a2+![]() a+2=
a+2=![]() a+
a+![]() .
.
即 a2﹣2a﹣6=0.
解得:a1=1+![]() ,a2=1﹣
,a2=1﹣![]() .
.
当a1=1+![]() 时,y=
时,y=![]() ×
×![]() (1+
(1+![]() )+
)+![]() =
=![]() .
.
∴P(![]() ,
,![]() ).
).
∵AP=A'P.
∴A'(2+![]() ,
,![]() ).
).
当a2=1﹣![]() 时,y=
时,y=![]() ×
×![]() (1﹣
(1﹣![]() )+
)+![]() =
=![]() .
.
∴P(![]() ,
,![]() ).
).
∵AP=AP'.
∴A'(2﹣![]() ,
,![]() ).
).
综上所述A'(2﹣![]() ,
,![]() ),(2+
),(2+![]() ,
,![]() ),(﹣1,0).
),(﹣1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】为全力助推句容建设,大力发展句容旅游,某公司拟派A、B两个工程队共同建设某区域的绿化带.已知A工程队2人与B工程队3人每天共完成310米绿化带,A工程队的5人与B工程队的6人每天共完成700米绿化带.
(1)求A队每人每天和B队每人每天各完成多少米绿化带;
(2)该公司决定派A、B工程队共20人参与建设绿化带,若每天完成绿化带总量不少于1480米,且B工程至少派出2人,则有哪几种人事安排方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,先描出点
 ,点
,点 .
.
(1)描出点
 关于
关于 轴的对称点
轴的对称点 的位置,写出
的位置,写出 的坐标 ;
的坐标 ;(2)用尺规在
 轴上找一点
轴上找一点 ,使
,使 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);(3)用尺规在
 轴上找一点
轴上找一点 ,使
,使 (保留作图痕迹).
(保留作图痕迹). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠ABC=30°,AC=3,动点D从点A出发,在AB边上以每秒1个单位的速度向点B运动,连结CD,作点A关于直线CD的对称点E,设点D运动时间为t(s).

(1)若△BDE是以BE为底的等腰三角形,求t的值;
(2)若△BDE为直角三角形,求t的值;
(3)当S△BCE≤
 时,求所有满足条件的t的取值范围(所有数据请保留准确值,参考数据:tan15°=2﹣
时,求所有满足条件的t的取值范围(所有数据请保留准确值,参考数据:tan15°=2﹣ ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A坐标(6,0),点B在y轴上,点C在第三象限角平分线上,动点P、Q同时从点O出发,点P以1cm/s 的速度沿O→A→B匀速运动到终点B;点Q沿O→C→B→A运动到终点A,点Q在线段OC、CB、BA上分别作匀速运动,速度分别为V1cm/s、V2cm/s、V3cm/s.设点P运动的时间为t(s),△OPQ的面积为S(cm2),已知S与t之间的部分函数关系如图(2)中的曲线段OE、曲线段EF和线段FG所示.
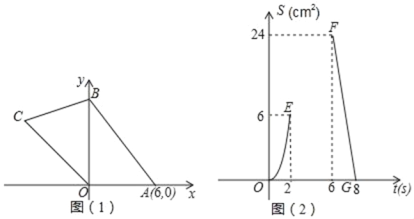
(1)V1= ,V2= ;
(2)求曲线段EF的解析式;
(3)补全函数图象(请标注必要的数据);
(4)当点P、Q在运动过程中是否存在这样的t,使得直线PQ把四边形OABC的面积分成11:13两部分,若存在直接写出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知等腰直角
 中,BD为斜边上的中线,E为DC上的一点,且
中,BD为斜边上的中线,E为DC上的一点,且 于G,AG交BD于F.
于G,AG交BD于F.(1)求证:AF=BE.
(2)如图②,当点E在DC的延长线上,其它条件不变,①的结论还能成立吗?若不能,请说明理由;若能,请予以证明。

相关试题

