【题目】如图(1),在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A坐标(6,0),点B在y轴上,点C在第三象限角平分线上,动点P、Q同时从点O出发,点P以1cm/s 的速度沿O→A→B匀速运动到终点B;点Q沿O→C→B→A运动到终点A,点Q在线段OC、CB、BA上分别作匀速运动,速度分别为V1cm/s、V2cm/s、V3cm/s.设点P运动的时间为t(s),△OPQ的面积为S(cm2),已知S与t之间的部分函数关系如图(2)中的曲线段OE、曲线段EF和线段FG所示.
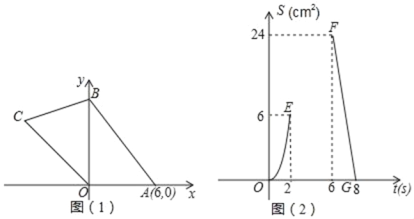
(1)V1= ,V2= ;
(2)求曲线段EF的解析式;
(3)补全函数图象(请标注必要的数据);
(4)当点P、Q在运动过程中是否存在这样的t,使得直线PQ把四边形OABC的面积分成11:13两部分,若存在直接写出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)3![]() ,
,![]() ;(2) S=
;(2) S=![]() t
t![]() =
=![]() t2+
t2+![]() t(2<t≤6;(3)见解析;(4)见解析.
t(2<t≤6;(3)见解析;(4)见解析.
【解析】
(1)观察图象可知,t=2时,点Q运动到点C位置,t=6时,点Q运动到点B位置.如图1中,作CE⊥x轴于E,CF⊥OB于F.利用图中信息,求出点C、B坐标即可解决问题.
(2)如图1中,当点Q在线段BC上时,作QN⊥OE于N,交CF于M.由QM∥BF,可得![]() =
=![]() ,推出
,推出![]() =
=![]() ,可得QM=
,可得QM=![]() ,QN=
,QN=![]() ,可得S=
,可得S=![]() t
t![]() =
=![]() t2+
t2+![]() t(2<t≤6).
t(2<t≤6).
(3)利用描点法即可解决问题;
(4)分两种情形构建方程即可解决问题;
解:(1)观察图象可知,t=2时,点Q运动到点C位置,t=6时,点Q运动到点B位置.
如图1中,作CE⊥x轴于E,CF⊥OB于F.
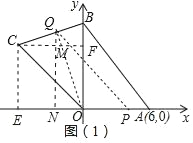
由题意6=![]() ×2×CE,
×2×CE,
∴CE=6,
∵∠COE=45°,
∴CE=OE=OF=CF=6,OC=6![]() ,
,
∴V1=![]() =3
=3![]() cm/s,
cm/s,
在Rt△CBF中,BC=![]() =2
=2![]() ,
,
∴V2=![]() =
=![]() cm/s,
cm/s,
故答案为3![]() ,
,![]() .
.
(2)如图1中,当点Q在线段BC上时,作QN⊥OE于N,交CF于M.
∵QM∥BF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QM=![]() ,QN=
,QN=![]() ,
,
∴S=![]() t
t![]() =
=![]() t2+
t2+![]() t(2<t≤6).
t(2<t≤6).
(3)在S=![]() t
t![]() =
=![]() t2+
t2+![]() t(2<t≤6)上取点(3,
t(2<t≤6)上取点(3,![]() ),(4,14),
),(4,14),
函数图象如图所示:
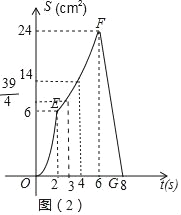
(4)如图3中,由题意满足条件的点Q在线段BC上,点P在线段OA上.
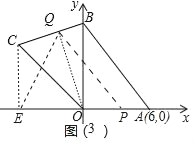
∵四边形AOCB的面积为48,
∴当四边形POCQ的面积=22或26时,满足条件,
∵S四边形POCQ=S△ECQ+S△PEQ,
<>则有:解得t=﹣17+![]() 或﹣17+3
或﹣17+3![]() (负根已经舍弃).
(负根已经舍弃).
∴t=﹣17+![]() 或﹣17+3
或﹣17+3![]() s时,直线PQ把四边形OABC的面积分成11:13两部分.
s时,直线PQ把四边形OABC的面积分成11:13两部分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,先描出点
 ,点
,点 .
.
(1)描出点
 关于
关于 轴的对称点
轴的对称点 的位置,写出
的位置,写出 的坐标 ;
的坐标 ;(2)用尺规在
 轴上找一点
轴上找一点 ,使
,使 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);(3)用尺规在
 轴上找一点
轴上找一点 ,使
,使 (保留作图痕迹).
(保留作图痕迹). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线l:y=
 x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.(1)求点A的坐标;
(2)求此二次函数的解析式;
(3)点P为直线l上一动点,将线段AC绕点P顺时针旋转α°(0°<α°<360°)得到线段A'C'(点A,A'是对应点,点C,C'是对应点).请问:是否存在这样的点P,使得旋转后点A'和点C'分别落在直线l和抛物线y=ax2﹣3ax+c的图象上?若存在,请直接写出点A'的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠ABC=30°,AC=3,动点D从点A出发,在AB边上以每秒1个单位的速度向点B运动,连结CD,作点A关于直线CD的对称点E,设点D运动时间为t(s).

(1)若△BDE是以BE为底的等腰三角形,求t的值;
(2)若△BDE为直角三角形,求t的值;
(3)当S△BCE≤
 时,求所有满足条件的t的取值范围(所有数据请保留准确值,参考数据:tan15°=2﹣
时,求所有满足条件的t的取值范围(所有数据请保留准确值,参考数据:tan15°=2﹣ ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知等腰直角
 中,BD为斜边上的中线,E为DC上的一点,且
中,BD为斜边上的中线,E为DC上的一点,且 于G,AG交BD于F.
于G,AG交BD于F.(1)求证:AF=BE.
(2)如图②,当点E在DC的延长线上,其它条件不变,①的结论还能成立吗?若不能,请说明理由;若能,请予以证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c).
(1)用这样的两个三角形构造成如图(2)的图形(B,E,C三点在一条直线上),利用这个图形,求证:a2+b2=c2
(2)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
请在坐标轴上找一点C,使△ABC为等腰三角形.
写出一个满足条件的在x轴上的点的坐标: ;
写出一个满足条件的在y轴上的点的坐标: ,这样的点有 个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
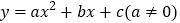 的图象如图所示,则下列结论:
的图象如图所示,则下列结论:①
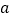 ,
, 同号;②当
同号;②当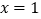 和
和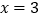 时,函数值相等;③
时,函数值相等;③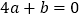 ;④当
;④当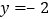 时,
时,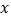 的值只能取
的值只能取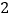 ;⑤当
;⑤当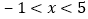 时,
时, .其中正确的有( )
.其中正确的有( )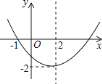
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

