【题目】如图1,菱形ABCD中,CH⊥AB,垂足为H,交对角线AC于M,连接BM,且AH=3.
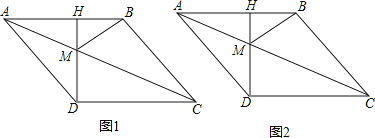
(1)求DM的长;
(2)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(3)在(2)的条件下,当点P在边AB上运动时,是否存在这样的t的值,使∠MPB与∠BCD互为余角?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)DM=![]() (2)S=-
(2)S=-![]() t+
t+![]() 或S=
或S=![]() t-
t-![]() .(3)存在,1.
.(3)存在,1.
【解析】
试题分析:(1)由菱形的性质得到条件,判断出△AMH∽△CDM,由勾股定理计算出DH,即可;
(2)由△BCM≌△DCM计算出BM=DM,分两种情况计算即可;
(3)由菱形的性质判断出△ADM≌△ABM,再判断出△BMP是等腰三角形,即可.
试题解析:(1)在Rt△ADH中,AD=5,AH=3,
∴DH=4,
∵四边形ABCD是菱形,
∴AB∥DC,
∴∠BAC=∠DCA,
DH⊥AB,
∴△AMH∽△CDM,
∴![]()
∴![]()
∵DH=4,
∴DM=![]()
(2)在△BCM和△DCM中,
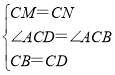
∴△BCM≌△DCM,
∴BM=DM=![]() ,∠CDM=∠CBM=90°
,∠CDM=∠CBM=90°
①当P在AB之间时,S=![]() (5-2t)×
(5-2t)×![]() =-
=-![]() t+
t+![]() .
.
②当P在BC之间时,S=![]() (2t-5)×
(2t-5)×![]() =
=![]() t-
t-![]() .
.
(3)存在,
∵∠ADM+∠BAD=90°,∠BCD=∠BAD,
∴∠ADM+∠BCD=90°,
∵∠MPB+∠BCD=90°,
∴∠MPB=∠ADM,
∵四边形ABCD是菱形,
∴∠DAM=∠BAM,
∵AM=AM,
∴△ADM≌△ABM,
∴∠ADM=∠ABM,
∴∠MPB=∠ABM,
∵MH⊥AB,
∴PH=BH=![]() ,
,
∴BP=2BH=3,
∵AB=5,
∴AP=2,
∴t=![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于上抛物体,在不计空气阻力的情况下,有如下关系式:h=v0t﹣
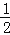 gt2,其中h(米)是上抛物体上升的高度,v0(米/秒)是上抛物体的初速度,g(米/秒2)是重力加速度,t(秒)是物体抛出后所经过的时间,如图是h与t的函数关系图.
gt2,其中h(米)是上抛物体上升的高度,v0(米/秒)是上抛物体的初速度,g(米/秒2)是重力加速度,t(秒)是物体抛出后所经过的时间,如图是h与t的函数关系图.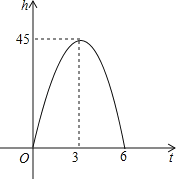
(1)求:v0和g;
(2)几秒后,物体在离抛出点40米高的地方?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.
(1)用含t的代数式表示P点对应的数:___________;
用含t的代数式表示点P和点C的距离:PC=_____________
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回点A,
①点P、Q同时运动运动的过程中有__________处相遇,相遇时t=_______________秒。
②在点Q开始运动后,请用t的代数式表示P、Q两点间的距离。(友情提醒:注意考虑P、Q的位置)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
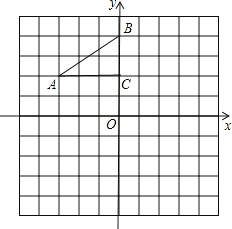
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:某商场因换季,将一品牌服装打折销售,每件服装如果按标价的六折出售将亏10元,而按标价的七五折出售将赚50元,问:
(1) 每件服装的标价是多少元?
(2) 每件服装的成本是多少元?
(3)为保证不亏本,最多能打几折?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x+2的值为1,则x等于( )
A.1 B.﹣1 C.3 D.﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中计算正确的是( )
A.(x+y)2=x2+y2
B.3x2=6x2
C.a2+a2=a4
D.(x2)3=x6
相关试题

