【题目】对于上抛物体,在不计空气阻力的情况下,有如下关系式:h=v0t﹣![]() gt2,其中h(米)是上抛物体上升的高度,v0(米/秒)是上抛物体的初速度,g(米/秒2)是重力加速度,t(秒)是物体抛出后所经过的时间,如图是h与t的函数关系图.
gt2,其中h(米)是上抛物体上升的高度,v0(米/秒)是上抛物体的初速度,g(米/秒2)是重力加速度,t(秒)是物体抛出后所经过的时间,如图是h与t的函数关系图.
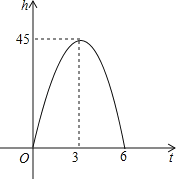
(1)求:v0和g;
(2)几秒后,物体在离抛出点40米高的地方?
参考答案:
【答案】(1)v0=30(米/秒),g=10(米/秒2);(2)经过2秒或4秒的物体在离抛出点40米高的地方.
【解析】
试题分析:(1)已知h=v0t﹣![]() gt2经过的坐标,把坐标代入解析式可解出v0和g;
gt2经过的坐标,把坐标代入解析式可解出v0和g;
(2)令h=40,代入方程可解.
解:(1)由图可知,h=v0t﹣![]() gt2的图象经过(6,0)、(3,45)点,
gt2的图象经过(6,0)、(3,45)点,
∴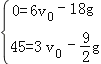 ,
,
解这个方程组,得:![]() .
.
∴v0=30(米/秒),g=10(米/秒2);
(2)由(1)得,函数关系式是h=30t﹣5t2,
当h=40时,则30t﹣5t2=40,
解这个方程,得t1=2,t2=4,
故经过2秒或4秒的物体在离抛出点40米高的地方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形的每个外角等于45°,则这个正多边形是( )
A. 正五边形 B. 正六边形 C. 正七边形 D. 正八边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】当n为整数时,(n+1)2﹣(n﹣1)2的值一定是4的倍数吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣6x﹣5=0配方组可变形为( )
A.(x﹣3)2=14 B.(x﹣3)2=4 C.(x+3)2=14 D.(x+3)2=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.
(1)用含t的代数式表示P点对应的数:___________;
用含t的代数式表示点P和点C的距离:PC=_____________
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回点A,
①点P、Q同时运动运动的过程中有__________处相遇,相遇时t=_______________秒。
②在点Q开始运动后,请用t的代数式表示P、Q两点间的距离。(友情提醒:注意考虑P、Q的位置)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
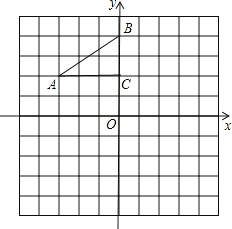
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,菱形ABCD中,CH⊥AB,垂足为H,交对角线AC于M,连接BM,且AH=3.
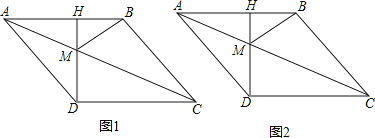
(1)求DM的长;
(2)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(3)在(2)的条件下,当点P在边AB上运动时,是否存在这样的t的值,使∠MPB与∠BCD互为余角?若存在,求出t的值;若不存在,请说明理由.
相关试题

