【题目】【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
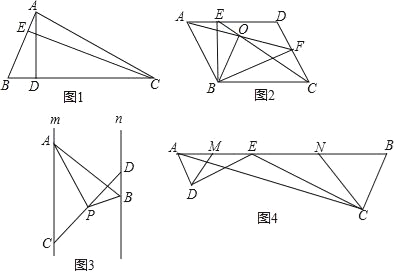
如图1,在△ABC中,AB=3,AD=6,问△ABC的高AD与CE的比是多少?
小聪的计算思路是:
根据题意得:S△ABC=![]() BCAD=
BCAD=![]() ABCE.
ABCE.
从而得2AD=CE,∴![]()
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
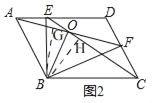
如图2,在ABCD中,点E、F分别在AD,CD上,且AF=CE,并相交于点O,连接BE、BF,
求证:BO平分角AOC.
(2)【探究延伸】
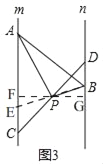
如图3,已知直线m∥n,点A、C是直线m上两点,点B、D是直线n上两点,点P是线段CD中点,且∠APB=90°,两平行线m、n间的距离为4.求证:PAPB=2AB.
(3)【迁移应用】
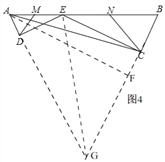
如图4,E为AB边上一点,ED⊥AD,CE⊥CB,垂足分别为D,C,∠DAB=∠B,AB=![]() ,BC=2,AC=
,BC=2,AC=![]() ,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
参考答案:
【答案】(1)见解析;(2)见解析;(3)5+![]()
【解析】分析:(1)、根据平行四边形的性质得出△ABF和△BCE的面积相等,过点B作OG⊥AF于G,OH⊥CE于H,从而得出AF=CE,然后证明△BOG和△BOH全等,从而得出∠BOG=∠BOH,即角平分线;(2)、过点P作PG⊥n于G,交m于F,根据平行线的性质得出△CPF和△DPG全等,延长BP交AC于E,证明△CPE和△DPB全等,根据等积法得出AB=![]() AP×PB,从而得出答案;(3)、,延长AD,BC交于点G,过点A作AF⊥BC于F,设CF=x,根据Rt△ABF和Rt△ACF的勾股定理得出x的值,根据等积法得出AE=2DM=2EM,BE=2CN=2EN, DM+CN=
AP×PB,从而得出答案;(3)、,延长AD,BC交于点G,过点A作AF⊥BC于F,设CF=x,根据Rt△ABF和Rt△ACF的勾股定理得出x的值,根据等积法得出AE=2DM=2EM,BE=2CN=2EN, DM+CN=![]() AB,从而得出两个三角形的周长之和.
AB,从而得出两个三角形的周长之和.
同理:EM+EN=![]() AB
AB
详解:证明:(1)如图2, ∵四边形ABCD是平行四边形,
∴S△ABF=![]() SABCD,S△BCE=
SABCD,S△BCE=![]() SABCD, ∴S△ABF=S△BCE,
SABCD, ∴S△ABF=S△BCE,
过点B作OG⊥AF于G,OH⊥CE于H, ∴S△ABF=![]() AF×BG,S△BCE=
AF×BG,S△BCE=![]() CE×BH,
CE×BH,
∴![]() AF×BG=
AF×BG=![]() CE×BH,即:AF×BG=CE×BH, ∵AF=CE, ∴BG=BH,
CE×BH,即:AF×BG=CE×BH, ∵AF=CE, ∴BG=BH,
在Rt△BOG和Rt△BOH中,![]() , ∴Rt△BOG≌Rt△BOH, ∴∠BOG=∠BOH,
, ∴Rt△BOG≌Rt△BOH, ∴∠BOG=∠BOH,
∴OB平分∠AOC,
(2)如图3,过点P作PG⊥n于G,交m于F, ∵m∥n, ∴PF⊥AC,
∴∠CFP=∠BGP=90°, ∵点P是CD中点,
在△CPF和△DPG中, , ∴△CPF≌△DPG, ∴PF=PG=
, ∴△CPF≌△DPG, ∴PF=PG=![]() FG=2,
FG=2,
延长BP交AC于E, ∵m∥n, ∴∠ECP=∠BDP, ∴CP=DP,
在△CPE和△DPB中, , ∴△CPE≌△DPB, ∴PE=PB,
, ∴△CPE≌△DPB, ∴PE=PB,
∵∠APB=90°, ∴AE=AB, ∴S△APE=S△APB,
∵S△APE=![]() AE×PF=AE=AB,S△APB=
AE×PF=AE=AB,S△APB=![]() AP×PB,
AP×PB,
∴AB=![]() AP×PB, 即:PAPB=2AB;
AP×PB, 即:PAPB=2AB;
(3)如图4,延长AD,BC交于点G, ∵∠BAD=∠B,
∴AG=BG,过点A作AF⊥BC于F,
设CF=x(x>0), ∴BF=BC+CF=x+2, 在Rt△ABF中,AB=![]() ,
,
根据勾股定理得,AF2=AB2﹣BF2=34﹣(x+2)2, 在Rt△ACF中,AC=![]() ,
,
根据勾股定理得,AF2=AC2﹣CF2=26﹣x2,
∴34﹣(x+2)2=26﹣x2, ∴x=﹣1(舍)或x=1, ∴AF=![]() =5,
=5,
连接EG, ∵S△ABG=![]() BG×AF=S△AEG+S△BEG=
BG×AF=S△AEG+S△BEG=![]() AG×DE+
AG×DE+![]() BG×CE=
BG×CE=![]() BG(DE+CE),
BG(DE+CE),
∴DE+CE=AF=5, 在Rt△ADE中,点M是AE的中点, ∴AE=2DM=2EM,
同理:BE=2CN=2EN, ∵AB=AE+BE, ∴2DM+2CN=AB, ∴DM+CN=![]() AB,
AB,
同理:EM+EN=![]() AB ∴△DEM与△CEN的周长之和=DE+DM+EM+CE+CN+EN=(DE+CE)+[(DM+CN)+(EM+EN)]
AB ∴△DEM与△CEN的周长之和=DE+DM+EM+CE+CN+EN=(DE+CE)+[(DM+CN)+(EM+EN)]
=(DE+CN)+AB=5+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A.
 B.
B. 
C.
 D.
D. 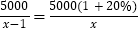
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,MA=MC,MB=MD,以AB为直径的O过点M且与DC延长线相切于点E.
(1)求证:四边形ABCD是菱形;
(2)若AB=4,求
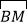 的长(结果请保留π)
的长(结果请保留π)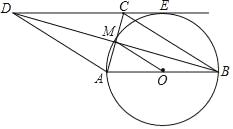
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣
 ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
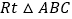 中,
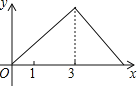
中,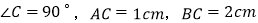 ,点P从点A出发,以
,点P从点A出发,以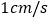 的速度沿折线
的速度沿折线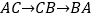 运动,最终回到点A,设点P的运动时间为
运动,最终回到点A,设点P的运动时间为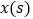 ,线段AP的长度为
,线段AP的长度为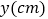 ,则能够反映y与x之间函数关系的图象大致是
,则能够反映y与x之间函数关系的图象大致是
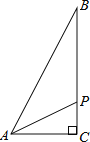
A.
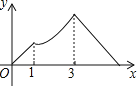 B.
B. 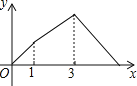
C.
 D.
D. 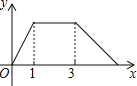
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,
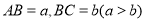 ,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.
,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.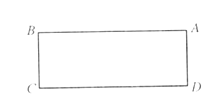
(1)画出长方形EFGD;
(2)连接BD、DF、BF,请用含有a、b的代数式表示
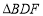 的面积;
的面积;(3)如果BF交CD于点H,请用含有a、b的代数式表示CH的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方形ABCD,点E在线段AD上,将
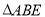 沿直线BE翻折后,点A落在线段CD上的点F.如果
沿直线BE翻折后,点A落在线段CD上的点F.如果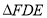 的周长为12,
的周长为12,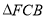 的周长为24,那么FC长为________.
的周长为24,那么FC长为________. 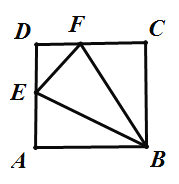
相关试题

