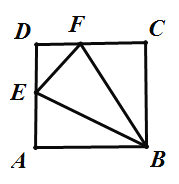
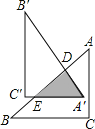
【题目】如图,已知长方形ABCD,点E在线段AD上,将![]() 沿直线BE翻折后,点A落在线段CD上的点F.如果
沿直线BE翻折后,点A落在线段CD上的点F.如果![]() 的周长为12,
的周长为12,![]() 的周长为24,那么FC长为________.
的周长为24,那么FC长为________.
参考答案:
【答案】6.
【解析】
由题意可得AE=EF,BF=AB=CD,根据△FDE的周长为12,△FCB的周长为24,可得DE+EF+DF=12,CF+BC+BF=24,等量代换后得CD+12- DF +CD-DF=24,于是可得(DC-DF)的值,即FC的长.
解:∵折叠后点A落在线段CD上的点F,
∴AE=EF,AB=BF,
∵四边形ABCD是长方形,
∴AD=BC,CD=AB,
∵△FDE的周长为12,△FCB的周长为24,
∴DE+EF+DF=12,BC+CF+FC=24,
∴DF+AD=12,AB+BC+CD-DF=24,
∴CD+12- DF +CD-DF=24,
∴CD-DF=6,
∴FC=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在△ABC中,AB=3,AD=6,问△ABC的高AD与CE的比是多少?
小聪的计算思路是:
根据题意得:S△ABC=
 BCAD=
BCAD= ABCE.
ABCE.从而得2AD=CE,∴
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在ABCD中,点E、F分别在AD,CD上,且AF=CE,并相交于点O,连接BE、BF,
求证:BO平分角AOC.
(2)【探究延伸】
如图3,已知直线m∥n,点A、C是直线m上两点,点B、D是直线n上两点,点P是线段CD中点,且∠APB=90°,两平行线m、n间的距离为4.求证:PAPB=2AB.
(3)【迁移应用】
如图4,E为AB边上一点,ED⊥AD,CE⊥CB,垂足分别为D,C,∠DAB=∠B,AB=
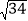 ,BC=2,AC=
,BC=2,AC=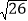 ,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.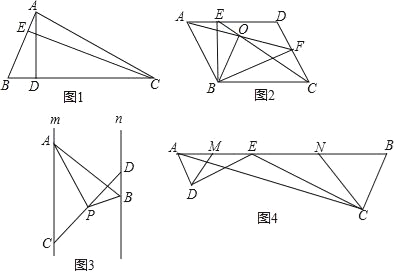
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
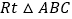 中,
中,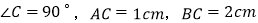 ,点P从点A出发,以
,点P从点A出发,以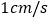 的速度沿折线
的速度沿折线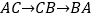 运动,最终回到点A,设点P的运动时间为
运动,最终回到点A,设点P的运动时间为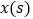 ,线段AP的长度为
,线段AP的长度为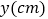 ,则能够反映y与x之间函数关系的图象大致是
,则能够反映y与x之间函数关系的图象大致是
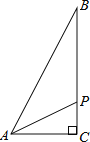
A.
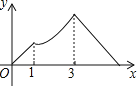 B.
B. 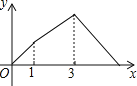
C.
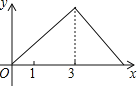 D.
D. 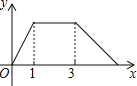
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,
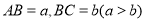 ,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.
,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.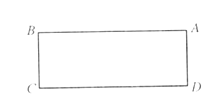
(1)画出长方形EFGD;
(2)连接BD、DF、BF,请用含有a、b的代数式表示
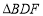 的面积;
的面积;(3)如果BF交CD于点H,请用含有a、b的代数式表示CH的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD和直线MN,点O在直线MN上.
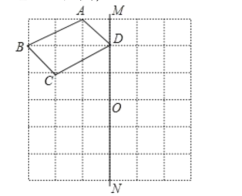
(1)画出四边形
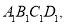 使四边形
使四边形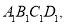 与四边形ABCD关于直线MN成轴对称;
与四边形ABCD关于直线MN成轴对称;(2)画出四边形
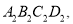 使四边形
使四边形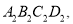 与四边形ABCD关于点O对称:
与四边形ABCD关于点O对称:(3)四边形
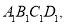 和四边形
和四边形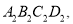 是轴对称和中心对称吗?若是,请在图上画出对称轴或对称中心.
是轴对称和中心对称吗?若是,请在图上画出对称轴或对称中心. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
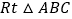 中,
中,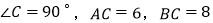 ,把
,把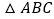 绕AB边上的点D顺时针旋转
绕AB边上的点D顺时针旋转 得到
得到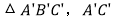 交AB于点E,若
交AB于点E,若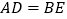 ,则
,则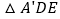 的面积是
的面积是
A. 3 B. 5 C. 11 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )

A、小莹的速度随时间的增大而增大B、小梅的平均速度比小莹的平均速度大
C、在起跑后180秒时,两人相遇D、在起跑后50秒时,小梅在小莹的前面
相关试题

