【题目】如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1). 
①先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1 , 试在图中画出Rt△A1B1C1 , 并写出点B1的坐标;
②再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2 , 试在图中画出Rt△A2B2C2 . 并写出点B2的坐标.
参考答案:
【答案】解:①所作图形如图所示:B1(﹣1,0)
②所作图形如图所示:B2(﹣4,﹣3).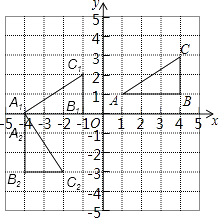
【解析】①分别将点A、B、C向左平移5个单位长度,再向下平移1个单位长度得到点A1、B1、C1 , 然后顺次连接;②分别将点B1、C1绕点A1顺时针旋转90°后得到点B2、C2 , 然后顺次连接,并写出点B2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE,连接BE,延长DE、BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.
(1)判断△ABE的形状,并证明你的结论;
(2)用含b代数式表示四边形ABFE的面积;
(3)求证:a2+b2=c2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在云南省某市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为:“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.

你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;扇形统计图中甲类部分的圆心是 .
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生2400人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读)如图1,四边形OABC中,OA=a,OC=3,BC=2,
∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(理解)
若点D与点A重合,则这个操作过程为FZ[45°,3];
(尝试)
(1)若点D恰为AB的中点(如图2),求θ;
(2)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,求出a的值;若点E落在四边形OABC的外部,直接写出a的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:四边形ABCD中,AB=CB=
 ,CD=
,CD= , DA=1,且AB⊥CB于B.
, DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;
(2)四边形ABCD的面积.

相关试题

