【题目】如图,动点M在以O为圆心,AB为直径的半圆弧上运动(点M不与点A、B 及 ![]() 的中点F 重合),连接OM.过点M 作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连接BM、BN.
的中点F 重合),连接OM.过点M 作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连接BM、BN.
(1)探究:如图一,当动点M在 ![]() 上运动时;
上运动时;
①判断△OEM∽△MDN是否成立?请说明理由;
②设 ![]() =k,k是否为定值?若是,求出该定值,若不是,请说明理由;
=k,k是否为定值?若是,求出该定值,若不是,请说明理由;
③设∠MBN=α,α是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如图二,当动点M 在 ![]() 上运动时;
上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)
参考答案:
【答案】
(1)
解:①△OEM∽△MDN成立,理由如下:
∵四边形BCDE是正方形,
∴BE=BC,∠EBC=∠CDE=∠BCD=∠BED=90°,
∴∠EOM+∠EMO=90°,
∵MN是⊙O的切线,
∴MN⊥OM,
∴∠OMN=90°,
∴∠DMN+∠EMO=90°,
∴∠EOM=∠DMN,
∴△OEM∽△MDN;
②k值为定值1;理由如下:
作BG⊥MN于G,如图一所示:
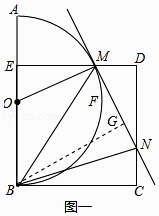
则BG∥OM,∠BGN=∠BGM=90°,
∴∠OMB=∠GBM,
∵OB=OM,
∴∠OBM=∠OMB,
∴∠OBM=∠GBM,
在△BME和△BMG中, 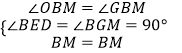 ,
,
∴△BME≌△BMG(AAS),
∴EM=GM,BE=BG,
∴BG=BC,
在Rt△BGN和Rt△BCN中, ![]() ,
,
∴Rt△BGN≌Rt△BCN(HL),
∴GN=CN,
∴EM+NC=GM+NC=MN,
∴k= ![]() =
= ![]() =1;
=1;
③设∠MBN=α,α为定值45°;理由如下:
∵△BME≌△BMG,Rt△BGN≌Rt△BCN,
∴∠EBM=∠GBM,∠GBN=∠CBN,
∴∠MBN= ![]() ∠EBC=45°,
∠EBC=45°,
即α=45°
(2)
解:(1)中的三个结论保持不变;理由同(1),
作BG⊥MN于G,如图二所示.

【解析】(1)①由正方形的性质得出BE=BC,∠EBC=∠CDE=∠BCD=∠BED=90°,由切线的性质和直角三角形的性质证出∠EOM=∠DMN,即可得出△OEM∽△MDN;②作BG⊥MN于G,则BG∥OM,∠BGN=∠BGM=90°,由平行线的性质和等腰三角形的性质得出∠OBM=∠GBM,由AAS证明△BME≌△BMG,得出EM=GM,BE=BG,证出BG=BC,由HL证明Rt△BGN≌Rt△BCN,得出GN=CN,证出EM+NC=GM+NC=MN,即可得出结论;③由全等三角形的性质得出∠EBM=∠GBM,∠GBN=∠CBN,求出∠MBN= ![]() ∠EBC=45°即可;(2)(1)中的三个结论保持不变;解法同(1).
∠EBC=45°即可;(2)(1)中的三个结论保持不变;解法同(1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠BAE=30°.(
 ≈1.4,
≈1.4,  ≈1.7)
≈1.7) 
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的解析式为y=﹣
 x2+bx+5.
x2+bx+5.
(1)当自变量 x≥2时,函数值y 随 x的增大而减少,求b 的取值范围;
(2)如图,若抛物线的图象经过点A(2,5),与x 轴交于点C,抛物线的对称轴与x 轴交于B.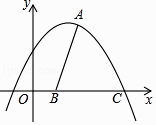
①求抛物线的解析式;
②在抛物线上是否存在点P,使得∠PAB=∠ABC?若存在,求出点P 的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年5月份,某市测得一周大气的PM2.5的日均值(单位:微克/立方米)如下:31,35,31,33,30,33,31.对于这组数据下列说法正确的是( )
A.众数是30
B.中位数是31
C.平均数是33
D.方差是32 -
科目: 来源: 题型:
查看答案和解析>>【题目】形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为( )

A.(﹣1, )
)
B.(0, )
)
C.( ,0)
,0)
D.(1, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
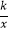 (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A.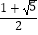
B.
C.
D.
相关试题

