【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22018+22019,①将等式两边同时乘2,得
2S=2+22+23+24+25+…+22019+22020,②
将②式减去①式,得2S-S=22020-1,
即S=22020-1,
则1+2+22+23+24+…+22019=22020-1.
请你仿照此法计算:
(1)1+2+22+23+24+…+210;
(2)1+3+32+33+34+…+3n(其中n为正整数).
参考答案:
【答案】(1) 211-1 ;(2)![]() .
.
【解析】
(1)设S=1+2+22+23+24+…+210,两边乘以2后得到关系式,与已知等式相减,变形即可求出所求式子的值;
(2)同理即可得到所求式子的值.
解:(1)设S=1+2+22+23+24+…+29+210,①
将等式两边同时乘2,得2S=2+22+23+24+…+210+211,②
将②式减去①式,得2S-S=211-1,即S=211-1,
则1+2+22+23+24+…+210=211-1.
(2)设S=1+3+32+33+34+…+3n-1+3n,①
将等式两边同时乘3,得3S=3+32+33+34+…+3n+3n+1,②
将②式减去①式,得3S-S=3n+1-1,即S=![]() ,
,
则1+3+32+33+34+…+3n=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017四川省达州市,第16题,3分)如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=
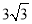 ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=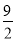 CE;④
CE;④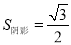 .其中正确结论的序号是__________.
.其中正确结论的序号是__________.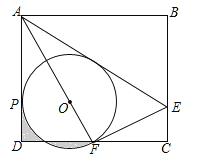
-
科目: 来源: 题型:
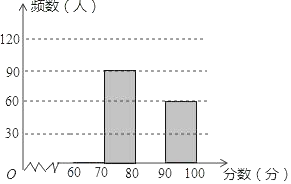
查看答案和解析>>【题目】为了了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题.
组别
分数段(分)
频数
百分率(%)
A组
60≤x<70
30
10
B组
70≤x<80
90
n
C组
80≤x<90
m
40
D组
90≤x<100
60
20
(1)样本容量a= ,表中m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”等,请你估计我县参加“科普知识”竞赛的1.5万名学生中成绩是“优”等的约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程(km)
﹣8
﹣11
﹣14
0
﹣16
+41
+8
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形
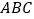 (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点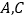 的坐标分别是
的坐标分别是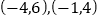 .
.(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出
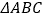 关于
关于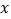 轴对称的
轴对称的 ;
;(3)请在
 轴上求作一点
轴上求作一点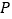 ,使
,使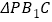 的周长最小,并写出点
的周长最小,并写出点 的坐标.
的坐标.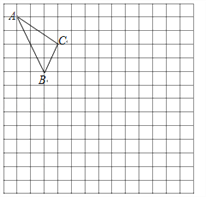
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜加工公司先后两批收购蒜苔(tái)共100吨,第一批蒜苔价格为1万元/吨;因蒜苔大量上市,第二批价格跌至0.4万元/吨,这两批蒜苔共用去52万元.
(1)求两批各购进蒜苔多少吨?
(2)公司收购后对蒜苔进行加工,分为粗加工和精加工两种.粗加工每吨利润400元,精加工每吨利润1600元要求精加工数量不大于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
相关试题

