【题目】在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD= . 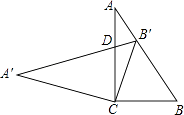
参考答案:
【答案】0.35
【解析】解:如图,过点C作CM⊥AB于点M,
∵∠C=90°,cosB= ![]() ,
,
∴ ![]() =
= ![]() ;设BC=3λ,则AB=5λ,
;设BC=3λ,则AB=5λ,
由勾股定理得AC=4λ,
由射影定理得:BC2=BMAB,
∴BM= ![]() λ.由旋转变换的性质得:
λ.由旋转变换的性质得:
CB=CB′,A′C=AC=4λ,∠A′=∠A;而CM⊥BB′,
∴B′M=BM,AB′=5λ﹣ ![]() λ=
λ= ![]() λ,
λ,
∵∠A′=∠A,∠A′DC=∠ADB′,
∴△A′DC∽△ADB′,
∴ ![]() =
= ![]() =0.35,
=0.35,
所以答案是:0.35;
【考点精析】本题主要考查了等腰三角形的性质和相似三角形的判定与性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2﹣(2m+1)x+2m不经过第三象限,且当x>2时,函数值y随x的增大而增大,则实数m的取值范围是( )
A.0≤m≤1.5
B.m≥1.5
C.0≤m≤1
D.0<m≤1.5 -
科目: 来源: 题型:
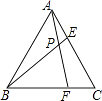
查看答案和解析>>【题目】如图,已知等边△ABC的边长为3,点E在AC上,点F在BC上,且AE=CF=1,则APAF的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商店出售同样的茶壶和茶杯,茶壶每只定价都是20元,茶杯每只定价都是5元.两家商店的优惠办法不同:甲商店是购买1只茶壶赠送1只茶杯;乙商店是按售价的92%收款.某顾客需购买4只茶壶、若干只(超过4只)茶杯,去哪家商店购买优惠更多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一般情况下,
 不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得
不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).(1)判断数对(﹣2,1),(3,3)是否是“相伴数对”;
(2)若(k,﹣1)是“相伴数对”,求k的值;
(3)若(4,m)是“相伴数对”,求代数式
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
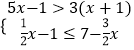 ,并把解集表示在数轴上.
,并把解集表示在数轴上.
相关试题

