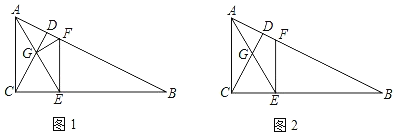
【题目】如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E为线段BC上一点,AE交CD于G,且GC=GE,EF⊥BC交AB于点F.
(1)求证:AE2=AFAB;
(2)连FG,若BE=2CE,求tan∠AFG;
(3)如图2,当tanB= 时,CE=FE(请直接写出结果,不需要解答过程).
参考答案:
【答案】(1)证明见解析;(2)tan∠AFG=![]() ;(3)
;(3)![]() .
.
【解析】
(1)先证明∠AEF=∠B,然后再证明△AEF∽△ABE,最后根据相似三角形的性质即可证明;
(2)设CE=a.则BE=2a,证明△AEC∽△BAC,得到AC=![]() a,易得∠AFG=60°,最后根据特殊角的三角函数值求解即可;
a,易得∠AFG=60°,最后根据特殊角的三角函数值求解即可;
(3)设BE=a,CE=EF=b,证明 △AEC∽△BAC.得到AC=![]() ,证明△BEF∽△BCA得到a、b的关系,最后根据正切的定义解答即可.
,证明△BEF∽△BCA得到a、b的关系,最后根据正切的定义解答即可.
(1)证明:∵GC=GE,
∴∠GCE=∠GEC,
∵CD⊥AB,
∴∠DCE+∠B=90°,
∵EF⊥BC,
∴∠GEC+∠AEF=90°,
∴∠AEF=∠B,又∠EAF=∠BAE,
∴△AEF∽△ABE,
∴![]() =
=![]() ,
,
∴AE2=AFAB;
(2)设CE=a,则BE=2a,
∵∠DCB+∠B=90°,∠CAB+∠B=90°,
∴∠DCB=∠CAB,
∵∠GCE=∠GEC,
∴∠CAB=∠GEC,又∠ACE=∠BCA=90°,
∴△AEC∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AC=![]() a,
a,
∴∠CAE=∠BAE=∠AEF=30°,
∴FA=FE,
∵∠GAC=∠GCA=30°,
∴GA=GC,
∵GC=GE,
∴GA=GE,又FA=FE,
∴∠AFG=60°,
∴tan∠AFG=![]() ;
;
(3)设BE=a,CE=EF=b,
∵△AEC∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AC2=b(a+b),
∴AC=![]() ,
,
∵EF∥AC,
∴△BEF∽△BCA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
整理得,b2+ab﹣a2=0,
则(![]() )2+
)2+![]() ﹣1=0,
﹣1=0,
解得:![]() =
=![]() ,
,
∴tanB=![]() =
=![]()
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列10×10的网格中,横、纵坐标均为整点的数叫做格点,例如A(﹣2,﹣2)、B(5,﹣3)、C(1,1)都是格点.
(1)∠ACB的大小为 ;
(2)要求在下图中仅用无刻度的直尺作图:以A为中心,取旋转角等于∠BAC.把△ABC逆时针旋转,得到△AB1C1,其中点C和点B的对应点分别为点C1和点B1,操作步骤如下:
第一步:延长AC到格点B1,使得AB1=AB;
第二步:延长BC到格点E,使得CE=CB,连接AE;
第三步:取格点F,连接FB1交AE于点C1,则△AB1C1即为所求.
请你按步骤完成作图,并直接写出B1、E、F三点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC为⊙O的直径,点D在BC上,AC=CD,∠ACB=2∠BAD
(1)求证:AB与⊙O相切;
(2)连接OD,若tanB=
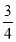 ,求tan∠ADO.
,求tan∠ADO.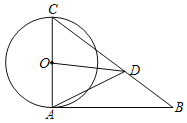
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径DE=10cm,△ABC中,∠ACB=90°,∠ABC=30°,BC=10cm,半圆O以1cm/s的速度从右到左运动,在运动过程中,D、E点始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的右侧,OC=6cm,那么,当t为_____s时,△ABC的一边所在直线与半圆O所在的圆相切.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B,C为数轴上的三点,如果点C在点A,B之间,且到点A的距离是点C到点B的距离的3倍,那么我们就称点C是{A,B}的奇妙点.例如,如图①,点A表示的数为-3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇妙点;又如,表示-2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇妙点.
(知识运用)
如图②,M,N为数轴上的两点,点M所表示的数为-2,点N所表示的数为6.
(1)表示数_____的点是{M,N}的奇妙点;表示数______的点是{N,M}的奇妙点;
(2)若点P所表示的数为3,点P是{M,N}的奇妙点,则点M、N所表示的数可以是几?M=______,N=_____(写出一组即可)
(3)如图③,A,B为数轴上的两点,点A所表示的数为-10,点B所表示的数为50.现有一动点P从点A出发向右运动,点P运动到数轴上的什么位置时,P,A,B中恰有一个点为其余两点的奇妙点?

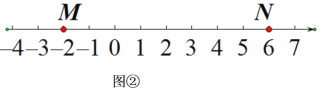
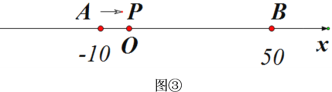
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2﹣2ax﹣3a与y轴交于C点,交x轴于A、B,且OB=OC.
(1)求抛物线的解析式;
(2)如图1,直线l:y=
 x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;
x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;(3)如图2,将原抛物线向左平移1个单位,向下平移t个单位,得到新抛物线C1.若直线y=m与新抛物线C1交于P、Q两点,点M是新抛物线C1上一动点,连接PM,并将直线PM沿y=m翻折交新抛物线C1于N,过Q作QT∥y轴,交MN于点T,求
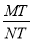 的值.
的值.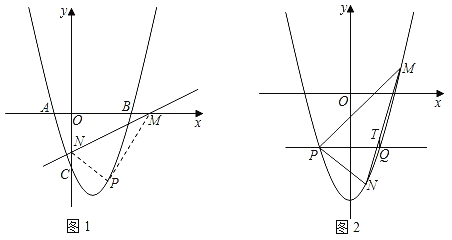
-
科目: 来源: 题型:
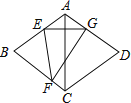
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,将菱形沿EF折叠,点B恰好落在AD边上的点G处,且EG⊥AC,若CD=8,则FG的长为( )
A. 6B.
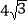 C. 8D.
C. 8D. 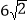
相关试题

