【题目】已知抛物线y=ax2﹣2ax﹣3a与y轴交于C点,交x轴于A、B,且OB=OC.
(1)求抛物线的解析式;
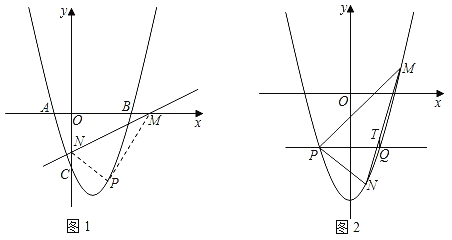
(2)如图1,直线l:y=![]() x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;
x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;
(3)如图2,将原抛物线向左平移1个单位,向下平移t个单位,得到新抛物线C1.若直线y=m与新抛物线C1交于P、Q两点,点M是新抛物线C1上一动点,连接PM,并将直线PM沿y=m翻折交新抛物线C1于N,过Q作QT∥y轴,交MN于点T,求![]() 的值.
的值.
参考答案:
【答案】(1)抛物线的表达式为y=x2﹣2x﹣3;(2)直线l的表达式为:y=![]() x﹣
x﹣![]() ;(3)1.
;(3)1.
【解析】
(1)OB=OC=3a,故点B(3a,0),将点B的坐标代入y=ax22ax3a,即可求解;
(2)求出点P的坐标(﹣![]() b,
b,![]() b),将点P的坐标代入抛物线表达式,即可求解;
b),将点P的坐标代入抛物线表达式,即可求解;
(3)计算xP+xM=k,同理可得:xP+xN=﹣k,而xT=xQ=﹣xP,而TH∥MG,故![]() ,即
,即![]() =
=![]() =1.
=1.
解:(1)∵c=﹣3a,
∴OB=OC=3a,故点B(3a,0),
将点B的坐标代入y=ax2﹣2ax﹣3a并解得:a=1或﹣![]() (舍去﹣
(舍去﹣![]() ),
),
故抛物线的表达式为:y=x2﹣2x﹣3;

(2)连接OP,交MN于点K,则OP⊥MN,
则直线OP的表达式为:y=﹣2x,而直线MN的表达式为:y=![]() x+b,
x+b,
联立上述两个表达式并解得:x=﹣![]() b,则点K(﹣
b,则点K(﹣![]() b,
b,![]() b),
b),
∵点K是OP的中点,由中点公式得:点P的坐标为(﹣![]() b,
b,![]() b),
b),
将点P的坐标代入抛物线表达式得:(﹣![]() b)2﹣2(﹣
b)2﹣2(﹣![]() b)﹣3=
b)﹣3=![]() b,解得:b=﹣
b,解得:b=﹣![]()
(不合题意值已舍去);
故直线l的表达式为: y=![]() x﹣
x﹣![]() ;
;
(3)平移后抛物线的表达式C1:y=x2﹣4﹣t①,
设直线PM的表达式为:y=kx+c②;则PN的表达式为:y=﹣kx+d,
联立①②并整理得:x2﹣kx﹣(4+t+c)=0,
∴xP+xM=k,
同理可得:xP+xN=﹣k,而xT=xQ=﹣xP,
如图2,过点N作x轴的平行线交过点M与y轴的平行线于点G,延长TQ交NG于点H,

∴TH∥MG,故![]() ,即
,即![]() =
=![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径DE=10cm,△ABC中,∠ACB=90°,∠ABC=30°,BC=10cm,半圆O以1cm/s的速度从右到左运动,在运动过程中,D、E点始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的右侧,OC=6cm,那么,当t为_____s时,△ABC的一边所在直线与半圆O所在的圆相切.

-
科目: 来源: 题型:
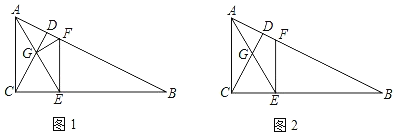
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E为线段BC上一点,AE交CD于G,且GC=GE,EF⊥BC交AB于点F.
(1)求证:AE2=AFAB;
(2)连FG,若BE=2CE,求tan∠AFG;
(3)如图2,当tanB= 时,CE=FE(请直接写出结果,不需要解答过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B,C为数轴上的三点,如果点C在点A,B之间,且到点A的距离是点C到点B的距离的3倍,那么我们就称点C是{A,B}的奇妙点.例如,如图①,点A表示的数为-3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇妙点;又如,表示-2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇妙点.
(知识运用)
如图②,M,N为数轴上的两点,点M所表示的数为-2,点N所表示的数为6.
(1)表示数_____的点是{M,N}的奇妙点;表示数______的点是{N,M}的奇妙点;
(2)若点P所表示的数为3,点P是{M,N}的奇妙点,则点M、N所表示的数可以是几?M=______,N=_____(写出一组即可)
(3)如图③,A,B为数轴上的两点,点A所表示的数为-10,点B所表示的数为50.现有一动点P从点A出发向右运动,点P运动到数轴上的什么位置时,P,A,B中恰有一个点为其余两点的奇妙点?

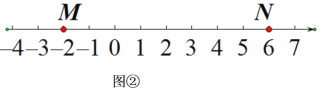
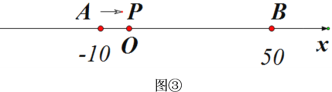
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,将菱形沿EF折叠,点B恰好落在AD边上的点G处,且EG⊥AC,若CD=8,则FG的长为( )
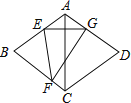
A. 6B.
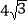 C. 8D.
C. 8D. 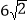
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填入相应的集合内:
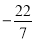 ,1.010010001,
,1.010010001,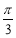 ,22,-8,
,22,-8,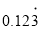 ,-1.232232223…,-1.414,0.
,-1.232232223…,-1.414,0.正数集合{ ……}
负数集合{ ……}
有理数集合{ ……}
无理数集合{ ……}
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习概率的课堂上,老师提出问题:一口袋装有除颜色外均相同的2个红球1个白球和1个篮球,小刚和小明想通过摸球来决定谁去看电影,同学甲设计了如下的方案:第一次随机从口袋中摸出一球(不放回);第二次再任意摸出一球,两人胜负规则如下:摸到“一红一白”,则小刚看电影;摸到“一白一蓝”,则小明看电影.
(1)同学甲的方案公平吗?请用列表或画树状图的方法说明;
(2)你若认为这个方案不公平,那么请你改变一下规则,设计一个公平的方案.
相关试题

