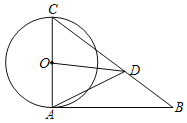
【题目】如图,△ABC中,AC为⊙O的直径,点D在BC上,AC=CD,∠ACB=2∠BAD
(1)求证:AB与⊙O相切;
(2)连接OD,若tanB=![]() ,求tan∠ADO.
,求tan∠ADO.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)设线段AD与⊙O交于E,连接CE,根据AC为⊙O的直径,可得CE⊥AD,再根据等腰三角形三线合一的性质可得∠ACD=2∠ACE,根据∠ACB=2∠BAD,从而得出∠ACE=∠DAB,再根据∠CAE=90°,可推出∠CAB=90°,即可证明AB与⊙O相切;
(2)延长CE交AB于M,则CM为AD的垂直平分线,连接DM,通过证明△ACM≌△DCM(SSS),可得∠BDM=90°,再根据锐角三角函数和中位线的性质求解即可.
(1)证明:设线段AD与⊙O交于E,连接CE,
∵AC为⊙O的直径,
∴CE⊥AD,
∵AC=CD,
∴∠ACD=2∠ACE,
∵∠ACB=2∠BAD,
∴∠ACE=∠DAB,
∵∠CAE=90°,
∴∠CAE+∠DAB=90,
∴∠CAB=90°,
∴AB与⊙O相切;
(2)解:∵AB与⊙O相切,
∴∠CAB=90°,
延长CE交AB于M,则CM为AD的垂直平分线,连接DM,
∴DM=AM,
∵AC=CD,CM=CM,
∴△ACM≌△DCM(SSS),
∴∠CDM=∠CAB=90°,
∴∠BDM=90°,
∵tanB=![]() ,
,
∴设AM=MD=3a,DB=4a,MB=5a,
AB=8a,AC=6a,
∴tan∠ACM=tan∠EAM=![]() ,
,
∴CE=2AE,AE=2EM,
设EN=k,
∴AE=DE=2k,CE=4k,
过O作ON⊥AD于N,
∴ON∥CE,
∴ON=![]() CE=2k,AN=
CE=2k,AN=![]() AE=k,
AE=k,
∴DN=3AN=3k,
∴tan∠ADO=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察算式:
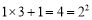 ;
;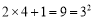 ;
;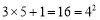 ;
;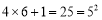 ,...请根据你发现的规律填空:
,...请根据你发现的规律填空:(1)
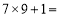 _________.
_________.(2)用含n 的等式表示上面的规律:__________.
(3)用找到的规律解决下面的问题:计算:
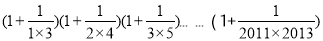 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】中华文化,源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:
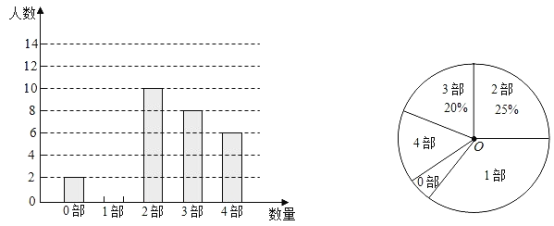
(1)请补全条形分布直方图,本次调查一共抽取了 名学生;
(2)扇形统计图中“1部”所在扇形的圆心角为 度;
(3)若该中学有1000名学生,请估计至少阅读3部四大古典名著的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列10×10的网格中,横、纵坐标均为整点的数叫做格点,例如A(﹣2,﹣2)、B(5,﹣3)、C(1,1)都是格点.
(1)∠ACB的大小为 ;
(2)要求在下图中仅用无刻度的直尺作图:以A为中心,取旋转角等于∠BAC.把△ABC逆时针旋转,得到△AB1C1,其中点C和点B的对应点分别为点C1和点B1,操作步骤如下:
第一步:延长AC到格点B1,使得AB1=AB;
第二步:延长BC到格点E,使得CE=CB,连接AE;
第三步:取格点F,连接FB1交AE于点C1,则△AB1C1即为所求.
请你按步骤完成作图,并直接写出B1、E、F三点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径DE=10cm,△ABC中,∠ACB=90°,∠ABC=30°,BC=10cm,半圆O以1cm/s的速度从右到左运动,在运动过程中,D、E点始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的右侧,OC=6cm,那么,当t为_____s时,△ABC的一边所在直线与半圆O所在的圆相切.

-
科目: 来源: 题型:
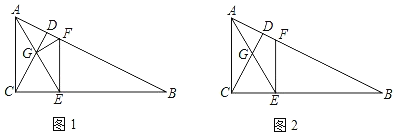
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E为线段BC上一点,AE交CD于G,且GC=GE,EF⊥BC交AB于点F.
(1)求证:AE2=AFAB;
(2)连FG,若BE=2CE,求tan∠AFG;
(3)如图2,当tanB= 时,CE=FE(请直接写出结果,不需要解答过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B,C为数轴上的三点,如果点C在点A,B之间,且到点A的距离是点C到点B的距离的3倍,那么我们就称点C是{A,B}的奇妙点.例如,如图①,点A表示的数为-3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇妙点;又如,表示-2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇妙点.
(知识运用)
如图②,M,N为数轴上的两点,点M所表示的数为-2,点N所表示的数为6.
(1)表示数_____的点是{M,N}的奇妙点;表示数______的点是{N,M}的奇妙点;
(2)若点P所表示的数为3,点P是{M,N}的奇妙点,则点M、N所表示的数可以是几?M=______,N=_____(写出一组即可)
(3)如图③,A,B为数轴上的两点,点A所表示的数为-10,点B所表示的数为50.现有一动点P从点A出发向右运动,点P运动到数轴上的什么位置时,P,A,B中恰有一个点为其余两点的奇妙点?

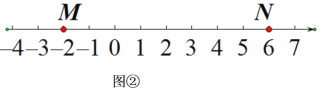
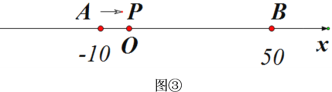
相关试题

