搜索
【题目】如图在平面直角坐标系xOy中，函数y1＝
(x＞0)的图象与一次函数y2＝kx－k的图象的交点为A(m，2)．
(1)求一次函数的解析式；
(2)设一次函数y＝kx－k的图象与y轴交于点B，若点P是x轴上一点，且满足△PAB的面积是6，请写出点P的坐标．
参考答案：
【答案】（1）y=2x-2 ;（2）P（-2,0）或（4,0）
【解析】
（1）将A点坐标代入y=
（x＞0），求出m的值为2，再将（2，2）代入y=kx-k，求出k的值，即可得到一次函数的解析式；
（2）将三角形以x轴为分界线，分为两个三角形计算，再把它们相加．
解：（1）将A（m，2）代入y=（x＞0）得，
m=2，
则A点坐标为A（2，2），
将A（2，2）代入y=kx-k得，2k-k=2，
解得k=2，则一次函数解析式为y=2x-2；
（2）∵一次函数y=2x-2与x轴的交点为C（1，0），与y轴的交点为B（0，-2），
S△ABP=S△ACP+S△BPC，
∴
×2CP+×2CP=6，
解得CP=3，
则P点坐标为（-2,0）或（4,0）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A，B，C三点在⊙O上，直径BD平分∠ABC，过点D作DE∥AB交弦BC于点E，在BC的延长线上取一点F，使得EF
DE．（1）求证：DF是⊙O的切线；
（2）连接AF交DE于点M，若 AD
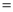4，DE
5，求DM的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】画图，探究：
（1）一个正方体组合图形的主视图、左视图（如图1）所示．
①这个几何体可能是（图2）甲、乙中的 ；
②这个几何体最多可由 个小正方体构成，请在图3中画出符合最多情况的一个俯视图．
（2）如图，已知一平面内的四个点A、B、C、D，根据要求用直尺画图．
①画线段AB，射线AD；
②找一点M，使M点即在射线AD上，又在直线BC上；
③找一点N，使N到A、B、C、D四个点的距离和最短．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，
， 
°，点D是线段BC上的动点，将线段AD绕点A顺时针旋转50°至
，连接
．已知AB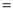
2cm，设BD为x cm，B
为y cm．
小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究，下面是小明的探究过程，请补充完整．（说明：解答中所填数值均保留一位小数）
（1）通过取点、画图、测量，得到了
与
的几组值，如下表： 
0.5
0.7
1.0
1.5
2.0
2.3
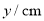
1.7
1.3
1.1
0.7
0.9
1.1
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．
（3）结合画出的函数图象，解决问题：
线段
的长度的最小值约为__________ 
；若
，则
的长度x的取值范围是_____________． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数
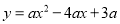．（1）该二次函数图象的对称轴是x
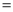；（2）若该二次函数的图象开口向下，当
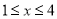时，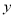 
的最大值是2，求当
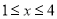时， 
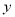的最小值；（3）若对于该抛物线上的两点
， 
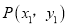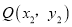，当
， 
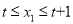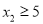时，均满足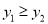
，请结合图象，直接写出
的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E．将点C翻折到对角线BD上的点N处，折痕DF交BC于点F．
（1）求证：四边形BFDE为平行四边形；
（2）若四边形BFDE为菱形，且AB＝2，求BC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于⊙C与⊙C上的一点A，若平面内的点P满足：射线AP与⊙C交于点Q（点Q可以与点P重合），且
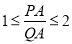，则点P称为点A关于⊙C的“生长点”．已知点O为坐标原点，⊙O的半径为1，点A（-1，0）．
（1）若点P是点A关于⊙O的“生长点”，且点P在x轴上，请写出一个符合条件的点P的坐标________；
（2）若点B是点A关于⊙O的“生长点”，且满足
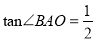，求点B的纵坐标t的取值范围；（3）直线
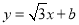与x轴交于点M，与y轴交于点N，若线段MN上存在点A关于⊙O的“生长点”，直接写出b的取值范围是_____________________________．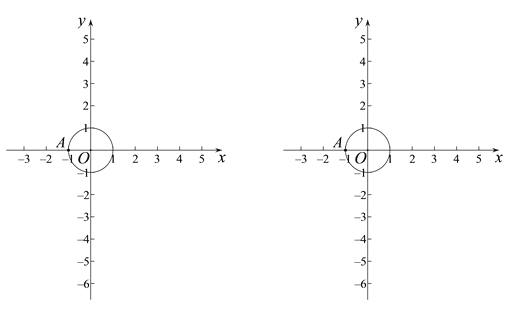
相关试题
