【题目】对于⊙C与⊙C上的一点A,若平面内的点P满足:射线AP与⊙C交于点Q(点Q可以与点P重合),且![]() ,则点P称为点A关于⊙C的“生长点”.
,则点P称为点A关于⊙C的“生长点”.
已知点O为坐标原点,⊙O的半径为1,点A(-1,0).
(1)若点P是点A关于⊙O的“生长点”,且点P在x轴上,请写出一个符合条件的点P的坐标________;
(2)若点B是点A关于⊙O的“生长点”,且满足![]() ,求点B的纵坐标t的取值范围;
,求点B的纵坐标t的取值范围;
(3)直线![]() 与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
参考答案:
【答案】(1)(2,0)(答案不唯一);(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:
(1)由题意可知,在x轴上找点P是比较简单的,这样的P点不是唯一的,如点(2,0)、(1,0)等;
(2)如图1,在x轴上方作射线AM交⊙O于点M,使tan∠MAO=![]() ,并在射线AM是取点N,使MN=AM,则由题意可知,线段MN上的点都是符合条件的B点,过点M作MH⊥x轴于点H,连接MC,结合已知条件求出点M和点N的纵坐标即可得到所求B点的纵坐标t的取值范围;根据对称性,在x轴的下方得到线段M′N′,同理可求得满足条件的B点的纵坐标t的另一取值范围;
,并在射线AM是取点N,使MN=AM,则由题意可知,线段MN上的点都是符合条件的B点,过点M作MH⊥x轴于点H,连接MC,结合已知条件求出点M和点N的纵坐标即可得到所求B点的纵坐标t的取值范围;根据对称性,在x轴的下方得到线段M′N′,同理可求得满足条件的B点的纵坐标t的另一取值范围;
(3)如图2,3,由![]() 与x轴交于点M,与y轴交于点N,可得点M的坐标为
与x轴交于点M,与y轴交于点N,可得点M的坐标为![]() ,点N的坐标为
,点N的坐标为![]() ,由此结合∠OMN的正切函数可求得∠OMN=60°;
,由此结合∠OMN的正切函数可求得∠OMN=60°;
以点D(1,0)为圆心,2为半径作圆⊙D,则⊙D和⊙O相切于点A,由题意可知,点A关于⊙O的“生长点”都在⊙O到⊙D之间的平面内,包括两个圆(但点A除外).
然后结合题意和∠OMN=60°分b>0和b<0两种情况在图2和图3中求出ON1和ON2的长即可得到b的取值范围了.
试题解析:
(1)由题意可知,在x轴上找点P是比较简单的,这样的P点不是唯一的,如点(2,0)、(1,0)等;
(2)如图1,在x轴上方作射线AM,与⊙O交于M,且使得![]() ,并在AM上取点N,使AM=MN,并由对称性,将MN关于x轴对称,得
,并在AM上取点N,使AM=MN,并由对称性,将MN关于x轴对称,得![]() ,则由题意,线段MN和
,则由题意,线段MN和![]() 上的点是满足条件的点B.
上的点是满足条件的点B.
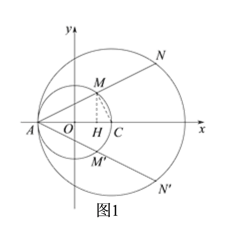
作MH⊥x轴于H,连接MC,
∴ ∠MHA=90°,即∠OAM+∠AMH=90°.
∵ AC是⊙O的直径,
∴ ∠AMC=90°,即∠AMH+∠HMC=90°.
∴ ∠OAM=∠HMC.
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ,解得
,解得![]() ,即点M的纵坐标为
,即点M的纵坐标为![]() .
.
又由![]() ,A为(-1,0),可得点N的纵坐标为
,A为(-1,0),可得点N的纵坐标为![]() ,
,
故在线段MN上,点B的纵坐标t满足: ![]() .
.
由对称性,在线段![]() 上,点B的纵坐标t满足:
上,点B的纵坐标t满足: ![]() .
.
∴ 点B的纵坐标t的取值范围是![]() 或
或![]() .
.
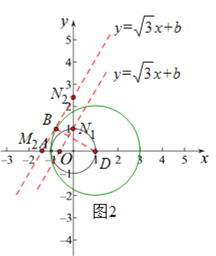
(3)如图2,以点D(1,0)为圆心,2为半径作圆⊙D,则⊙D和⊙O相切于点A,由题意可知,点A关于⊙O的“生长点”都在⊙O到⊙D之间的平面内,包括两个圆(但点A除外).
∵直线![]() 与x轴交于点M,与y轴交于点N,
与x轴交于点M,与y轴交于点N,
∴点M的坐标为![]() ,点N的坐标为
,点N的坐标为![]() ,
,
∴tan∠OMN=![]() ,
,
∴∠OMN=60°,
要在线段MN上找点A关于⊙O的“生长点”,现分“b>0”和“b<0”两种情况讨论:
I、①当直线![]() 过点N1(0,1)时,线段MN上有点A关于⊙O的唯一“生长点”N1,此时b=1;
过点N1(0,1)时,线段MN上有点A关于⊙O的唯一“生长点”N1,此时b=1;
②当直线![]() 与⊙D相切于点B时,线段MN上有点A关于⊙O的唯一“生长点”B,此时直线
与⊙D相切于点B时,线段MN上有点A关于⊙O的唯一“生长点”B,此时直线![]() 与y轴相交于点N2,与x轴相交于点M2,连接DB,则DB=2,
与y轴相交于点N2,与x轴相交于点M2,连接DB,则DB=2,
∴DM2=![]() ,
,
∴OM2=![]() ,
,
∴ON2=tan60°·OM2=![]() ,此时b=
,此时b=![]() .
.
综合①②可得,当b>0时,若线段MN上存在点A关于⊙O的“生长点”,则b的取值范围为: ![]() ;
;
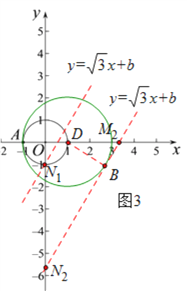
II、当b<0时,如图3,同理可得若线段MN上存在点A关于⊙O的“生长点”,则b的取值范围为: ![]() ;
;
综上所述,若在线段MN上存在点A关于⊙O的“生长点”,则b的取值范围为: ![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系xOy中,函数y1=
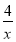 (x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
(x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是6,请写出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
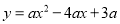 .
.(1)该二次函数图象的对称轴是x
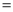 ;
;(2)若该二次函数的图象开口向下,当
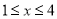 时,
时, 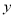 的最大值是2,求当
的最大值是2,求当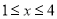 时,
时, 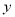 的最小值;
的最小值;(3)若对于该抛物线上的两点
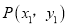 ,
, 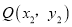 ,当
,当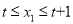 ,
, 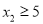 时,均满足
时,均满足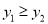 ,请结合图象,直接写出
,请结合图象,直接写出 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.

(1)求证:四边形BFDE为平行四边形;
(2)若四边形BFDE为菱形,且AB=2,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A
 90°,AB
90°,AB AC.
AC.(1)如图1,△ABC的角平分线BD,CE交于点Q,请判断“
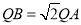 ”是否正确:________(填“是”或“否”);
”是否正确:________(填“是”或“否”);(2)点P是△ABC所在平面内的一点,连接PA,PB,且PB

 PA.
PA.①如图2,点P在△ABC内,∠ABP
 30°,求∠PAB的大小;
30°,求∠PAB的大小;②如图3,点P在△ABC外,连接PC,设∠APC
 α,∠BPC
α,∠BPC β,用等式表示α,β之间的数量关系,并证明你的结论.
β,用等式表示α,β之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织部分师生从学校(A地)到300千米外的B地进行红色之旅(革命传统教育),租用了客运公司甲、乙两辆车,其中乙车速度是甲车速度的
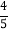 ,两车同时从学校出发,以各自的速度匀速行驶,行驶2小时后甲车到达服务区C地,此时两车相距40千米,甲车在服务区休息15分钟户按原速度开往B地,乙车行驶过程中未做停留.
,两车同时从学校出发,以各自的速度匀速行驶,行驶2小时后甲车到达服务区C地,此时两车相距40千米,甲车在服务区休息15分钟户按原速度开往B地,乙车行驶过程中未做停留.(1)求甲、乙两车的速度?
(2)问甲车在C地结束休息后再行驶多长时间,甲、乙两车相距30千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
相关试题

