【题目】如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.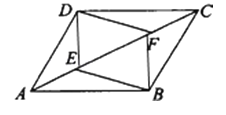
参考答案:
【答案】证明:连接BD,交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形DEBF是平行四边形.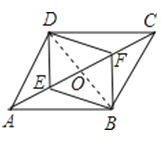
【解析】首先连接BD,交AC于点O,由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,即可求得OA=OC,OB=OD,又由AE=CF,可得OE=OF,然后根据对角线互相相平分的四边形是平行四边形.
【考点精析】本题主要考查了全等三角形的性质和平行四边形的判定与性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某九年级制学校围绕“每天30分钟的大课间,你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:
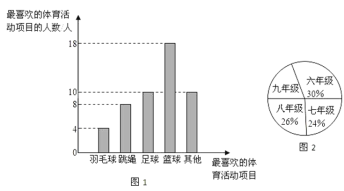
(1)该校对多少学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD.

(1)图中除直角外,请写出一对相等的角吗:(写出符合的一对即可)
(2)如果∠AOE=26°,求∠BOD和∠COF的度数.(所求的角均小于平角) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的方程mx2=3有两个实数根,那么m的取值范围是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. (x3)2=x5 B. (-x)5=-x5
C. x3·x2=x6 D. 3x2+2x3=5x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校组织植树活动,已知在甲处植树的有14人,在乙处植树的有6人,现调70人去支援.
(1)若要使在甲处植树的人数与在乙处植树的人数相等,应调往甲处人.
(2)若要使在甲处植树的人数是在乙处植树人数的2倍,问应调往甲、乙两处各多少人?
(3)通过适当的调配支援人数,使在甲处植树的人数恰好是在乙处植树人数的n倍(n是大于1的正整数,不包括1.)则符合条件的n的值共有个. -
科目: 来源: 题型:
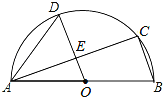
查看答案和解析>>【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=72°,求∠CAD的度数;
(2)若AB=13,AC=12,求DE的长.
相关试题

