【题目】学校组织植树活动,已知在甲处植树的有14人,在乙处植树的有6人,现调70人去支援.
(1)若要使在甲处植树的人数与在乙处植树的人数相等,应调往甲处人.
(2)若要使在甲处植树的人数是在乙处植树人数的2倍,问应调往甲、乙两处各多少人?
(3)通过适当的调配支援人数,使在甲处植树的人数恰好是在乙处植树人数的n倍(n是大于1的正整数,不包括1.)则符合条件的n的值共有个.
参考答案:
【答案】
(1)31
(2)解:解:设调往甲处x人,则调往乙处(70﹣x)人,由题意得:
14+x=2(6+70﹣x),
解得:x=46
成人数:70﹣46=24(人),
答:应调往甲处46人,乙处24人
(3)6
【解析】解:(1)设调往甲处y人,则调往乙处(70﹣y)人,由题意得:
14+y=6+(70﹣y),
解得:y=31,
故答案为:31;(3)设调往甲处z人,则调往乙处(70﹣z)人,列方程得
14+z=n(6+70﹣z),
14+z=n(76﹣z),
n= ![]() ,
,
解得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
共6种,
故答案为:6.
(1)设调往甲处y人,则调往乙处(70﹣y)人,由题意得等量关系:在甲处植树的人数=在乙处植树的人数,根据等量关系列出方程,再解即可;(2)设调往甲处x人,则调往乙处(70﹣x)人,由题意得等量关系:在甲处植树的人数=在乙处植树的人数×2,根据等量关系列出方程,再解即可;(3)设调往甲处z人,则调往乙处(70﹣z)人,由题意得等量关系:在甲处植树的人数=在乙处植树的人数×n,根据等量关系列出方程,再求出整数解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.

(1)若∠DOF=25°,求∠AOB的度数.
(2)若OA平分∠BOE,则∠DOF的度数是 . (直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】能说明命题“若a>b,则3a>2b“为假命题的反例为( )
A.a=3,b=2B.a=﹣2,b=﹣3C.a=2,b=3D.a=﹣3,b=﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】为体现社会对老师的尊重,教师节这一天上午,出租车司机小王在东西向的公路上免费接送老师,如果规定向东为正,向西为负,出租车的行程如下(单位:千米):+5,﹣4,+3,﹣10,+3,﹣9
最后一名老师送到目的地,小王距出租车出发点的距离是多少?在出发点的哪个方向?
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3πxyz2的系数是 , 次数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+5|+(b﹣4)2=0,则(a+b)2016= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0.
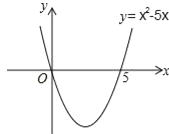
解:设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法写出一元二次不等式的解集:x2﹣2x﹣3>0. .
相关试题

