【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)b= , c= , 点B的坐标为;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
参考答案:
【答案】
(1)-2;-3;(﹣1,0)
(2)
解:存在.
理由:如图所示:
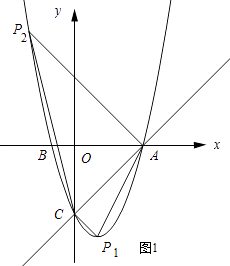
①当∠ACP1=90°.
由(1)可知点A的坐标为(3,0).
设AC的解析式为y=kx﹣3.
∵将点A的坐标代入得3k﹣3=0,解得k=1,
∴直线AC的解析式为y=x﹣3.
∴直线CP1的解析式为y=﹣x﹣3.
∵将y=﹣x﹣3与y=x2﹣2x﹣3联立解得x1=1,x2=0(舍去),
∴点P1的坐标为(1,﹣4).
②当∠P2AC=90°时.
设AP2的解析式为y=﹣x+b.
∵将x=3,y=0代入得:﹣3+b=0,解得b=3.
∴直线AP2的解析式为y=﹣x+3.
∵将y=﹣x+3与y=x2﹣2x﹣3联立解得x1=﹣2,x2=3(舍去),
∴点P2的坐标为(﹣2,5).
综上所述,P的坐标是(1,﹣4)或(﹣2,5).
(3)
解:如图2所示:连接OD.

由题意可知,四边形OFDE是矩形,则OD=EF.
根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短.
由(1)可知,在Rt△AOC中,
∵OC=OA=3,OD⊥AC,
∴D是AC的中点.
又∵DF∥OC,
∴DF= ![]() OC=
OC= ![]() .DF=
.DF= ![]() OC=
OC= ![]()
∴点P的纵坐标是- ![]() .
.
∴ ![]() ,解得:
,解得: ![]() .
.
∴当EF最短时,点P的坐标是:( ![]() ,-
,- ![]() )或(
)或( ![]() ,-
,- ![]() ).
).
【解析】解:(1)∵将点A和点C的坐标代入抛物线的解析式得: ![]() ,解得:b=﹣2,c=﹣3.
,解得:b=﹣2,c=﹣3.
∴抛物线的解析式为y=x2﹣2x﹣3.
∵令x2﹣2x﹣3=0,解得:x1=﹣1,x2=3.
∴点B的坐标为(﹣1,0).
所以答案是:﹣2;﹣3;(﹣1,0).
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点和垂线段最短的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请将下列证明过程补充完整:
已知:如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2
求证:∠E=∠F

证明:∵∠BAP+∠APD=180°(已知)
∴ ∥ ( )
∴∠BAP= ( )
又∵∠1=∠2(已知)
∴∠BAP﹣ = ﹣∠2
即∠3= (等式的性质)
∴AE∥PF( )
∴∠E=∠F( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D把一个400米的环形跑道分成相等的4段,即两条直道和两条弯道的长度相同.甲平均每秒跑4米,乙平均每秒跑6米,若甲、乙两人分别从A、C两处同时相向出发(如图),当他们第4次相遇时,其相遇点在____________段(填”AB”或”BC”或”CD”或”DA”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张长方形纸片分别沿着EP,FP对折,使B落在B′,C落在C′.
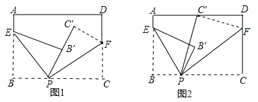
(1)若点P,B′,C′在同一直线上(图1),求两条折痕的夹角∠EPF的度数;
(2)若点P,B′,C′不在同一直线上(图2),且∠B′PC′=10°,求∠EPF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全是老百姓关注的话题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( )

A.1:4
B.1:3
C.1:2
D.1:1 -
科目: 来源: 题型:
查看答案和解析>>【题目】历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)来表示.例如f(x)=x2+3x-5,把x=某数时多项式的值用f(某数)来表示.例如x=-1时多项式x2+3x-5的值记为f(-1)=(-1)2+3×(-1)-5=-7.
(1)已知g(x)=-2x2-3x+1,分别求出g(-1)和g(-2);
(2)已知h(x)=ax3+2x2-ax-6,当h(
 )=a,求a的值;
)=a,求a的值;(3)已知f(x)=
 -
- -2(a,b为常数),当k无论为何值,总有f(1)=0,求a,b的值.
-2(a,b为常数),当k无论为何值,总有f(1)=0,求a,b的值.
相关试题

