【题目】如图,有人在岸上点C的地方,用绳子拉船靠岸开始时,绳长CB=5米,拉动绳子将船身向岸边行驶了2米到点D后,绳长CD=![]() 米,求岸上点C离水面的高度CA.
米,求岸上点C离水面的高度CA.

参考答案:
【答案】3米.
【解析】试题分析:
设AD= ![]() 米,则由题意可知:AB=BD+AD=
米,则由题意可知:AB=BD+AD=![]() 米,∠CAB=90°,由此根据勾股定理可得:在Rt△ABC中,AC2=CB2-AB2,在Rt△ADC中,AC2=CD2-AD2,由此可得:CB2-AB2=CD2-AD2,即:
米,∠CAB=90°,由此根据勾股定理可得:在Rt△ABC中,AC2=CB2-AB2,在Rt△ADC中,AC2=CD2-AD2,由此可得:CB2-AB2=CD2-AD2,即: ![]() ,解方程求得
,解方程求得![]() 的值,将所求
的值,将所求![]() 的值代入:AC2=CD2-AD2即可求得AC的值.
的值代入:AC2=CD2-AD2即可求得AC的值.
试题解析:
由题意可知:∠CAB=90°,
∴在Rt△ABC中,AC2=CB2-AB2,在Rt△ADC中,AC2=CD2-AD2,
∴CB2-AB2=CD2-AD2.
设AD= ![]() 米,则由题意可知:AB=BD+AD=
米,则由题意可知:AB=BD+AD=![]() 米,
米,
∴![]() ,解得:
,解得: ![]() ,即AD=2米.
,即AD=2米.
∴AB=2+2=4(米),
∴AC2=CB2-AB2=25-16=9,
∴AC=3(米).
答:点C离水面高度AC为3米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在图中正确作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 ,△A′B′C′的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,y1)、B(2,y2)都在直线y=﹣2x+3上,则y1与y2的大小关系是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB.
(1)求两个函数的解析式;
(2)求△AOB的面积;
(3)在x轴上存在一点p,使△AOP是等腰三角形,直接写出所有符合要求的点P的坐标.

-
科目: 来源: 题型:
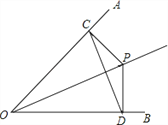
查看答案和解析>>【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.
-
科目: 来源: 题型:
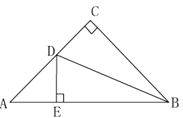
查看答案和解析>>【题目】如图,已知:在△ABC中,∠C=90°,AC=BC,BD平分∠CBA,DE⊥AB于点E.
求证:AD+DE=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kx+4是一个完全平方式,则整数k的值为_____.
相关试题

