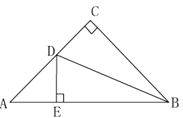
【题目】如图,已知:在△ABC中,∠C=90°,AC=BC,BD平分∠CBA,DE⊥AB于点E.
求证:AD+DE=BE.
参考答案:
【答案】证明见解析.
【解析】试题分析:(1)由∠DEB=∠C,∠EBD=∠CBD,DB=DB可得△DEB≌△DCB,所以BC=BE,又因为AC=BC,所以AC=BE,由题意可得,△ABC为等腰直角三角形,故不难得出△ADE为等腰直角三角形,所以AE=DE,所以AD+DE=AD+DC=AC=BC=BE.
试题解析:
∵BD平分∠CBA,
∴∠EBD=∠CBD,
∵DE⊥AB,
∴∠DEB=90°,
∵∠C=90°,
∴∠DEB=∠C,
在△DEB和△DCB中:
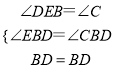 ,
,
∴△DEB≌△DCB(AAS),
∴DE=DC,BE=BC,
∵AD+DE=AD+DC=AC=BC,
∴AD+DE=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB.
(1)求两个函数的解析式;
(2)求△AOB的面积;
(3)在x轴上存在一点p,使△AOP是等腰三角形,直接写出所有符合要求的点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有人在岸上点C的地方,用绳子拉船靠岸开始时,绳长CB=5米,拉动绳子将船身向岸边行驶了2米到点D后,绳长CD=
 米,求岸上点C离水面的高度CA.
米,求岸上点C离水面的高度CA.
-
科目: 来源: 题型:
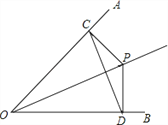
查看答案和解析>>【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kx+4是一个完全平方式,则整数k的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某儿童服装店欲购进A、B两种型号的儿童服装;经调查:B型号童装的进货单价是A型号童装的进货单价的两倍,购进A型号童装60件和B型号童装40件共用去2100元.
求A、B两种型号童装的进货单价各是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程
 的两根.
的两根.(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.

相关试题

