【题目】如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD. 
参考答案:
【答案】证明:在AB上取一点F,使AF=AC,连结EF. 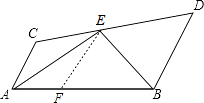
∵EA、EB分别平分∠CAB和∠DBA,
∴∠CAE=∠FAE,∠EBF=∠EBD.
∵AC∥BD,
∴∠C+∠D=180°.
在△ACE和△AFE中,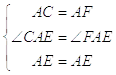 ,
,
∴△ACE≌△AFE(SAS),
∴∠C=∠AFE.
∵∠AFE+∠EFB=180°,
∴∠EFB=∠D.
在△BEF和△BED中,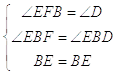 ,
,
∴△BEF≌△BED(AAS),
∴BF=BD.
∵AB=AF+BF,
∴AB=AC+BD.
【解析】在AB上取一点F,使AF=AC,连结EF,就可以得出△ACE≌△AFE,就有∠C=∠AFE.由平行线的性质就有∠C+∠D=180°,由∠AFE+∠EFB=180°得出∠EFB=∠D,在证明△BEF≌△BED就可以得出BF=BD,进而就可以得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程(a-b)x2+(b-c)x+(c-a)=0是关于x的一元二次方程,则必有( )
A.a=b=c
B.一根为1
C.一根为-1
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,DE垂直平分AC,D为垂足,交AB于E,连接CE.
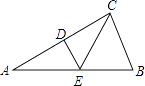
(1)求∠ECB的度数;
(2)若AB=10,求△BCE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
则这100名同学平均每人植树_____棵;若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总数是______棵.
植树数量(单位:棵)
4
5
6
8
10
人数
28
20
25
16
11
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程 x2= x的根是( )
A. x1=0,x2=1 B. x1=0,x2=-1 C. x1=x2=0 D. x1=x2=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2?a3=a6
B.(﹣2xy2)3=﹣8x3y5
C.2a﹣3=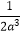
D.(﹣a)3÷(2a)2=﹣ a
a
相关试题

