【题目】如图1,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B,C在AE的异侧,BD⊥AE于D,CE⊥AE于E.

(1)△ABD与△CAE全等吗?BD与DE+CE相等吗?请说明理由。
(2)如图2,若直线AE绕点A旋转到图②所示的位置(BD<CE)时,其余条件不变,则BD与DE、CE的关系如何?请说明理由
(3)如图3,若直线AE绕点A旋转到图③所示的位置(BD>CE)时,其余条件不变,则BD与DE、CE的关系如何?
(4)根据以上的讨论,请用简洁的语言表达BD与DE、CE的数量关系.
参考答案:
【答案】(1)见解析;(2)BD=DE-CE,理由见解析; (3)BD=DE-CE;理由见解析;(4) 当点B、C在AE异侧时,BD=DE+CE;当点B、C在AE同侧时,BD=DE-CE.
【解析】
(1)在直角三角形中,由题中条件可得∠ABD=EAC,又有AB=AC,则有一个角及斜边相等,则可判定Rt△BAD≌Rt△AEC,由三角形全等可得三角形对应边相等,进而通过线段之间的转化,可得出结论;
(2)由题中条件同样可得出Rt△BAD≌Rt△AEC,得出对应线段相等,进而可得线段之间的关系;
(3)同(2)的方法即可得出结论.
(4)利用(1)(2)(3)即可得出结论.
(1)证明:在△ABD和△CAE中,
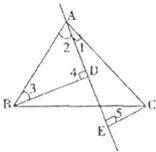
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
又∠4=∠5=90°,AB=AC,
∴△ABD≌△CAE.(AAS),
∴BD=AE,AD=CE.
又AE=AD+DE,
∴AE=DE+CE,
即BD=DE+CE.
(2)BD=DE-CE.
证明:∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
又∵BD⊥DE,∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.
又AB=AC,∠ADB=∠CEA=90°,
∴△ADB≌△CEA.
∴BD=AE,AD=CE.
∵DE=AD+AE,
∴DE=CE+BD,
即BD=DE-CE.
(3)同(2)的方法可证:BD=DE-CE.
(4)当点B、C在AE异侧时,BD=DE+CE;当点B、C在AE同侧时,BD=DE-CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请用两种不同的方法列代数式表示图中阴影部分的面积.

方法①_________________;
方法②_________________;
(2)根据(1)写出一个等式________________;
(3)若
 ,
, .
.①求
 的值。
的值。②
 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平底面A处安置测角仪测一得楼房CD顶部点CD的仰角为45°,向前走20米到达A1处,测得点D的仰角为67.5°.已知测角仪AB的高度为1米,则楼房CD的高度为( )
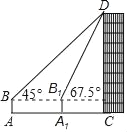
A. (
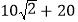 )米 B. (
)米 B. (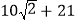 )米 C. (
)米 C. (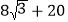 )米 D. (
)米 D. (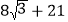 )米
)米 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以点M(6,8)为圆心,2为半径的圆上有一动点P,若A(﹣2,0),B(2,0),连接PA,PB,则当PA2+PB2取得最大值时,PO的长度为( )
A. 8 B. 10 C. 12 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用直尺和圆规作一个角∠A′O′B′,等于已知角∠AOB,能得出∠A′O′B′=∠AOB的依据是( )

A.SASB.ASAC.AASD.SSS
-
科目: 来源: 题型:
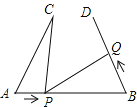
查看答案和解析>>【题目】如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA=60°,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s),则点Q的运动速度为 cm/s,使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:全等三角形对应的角平分线相等。
相关试题

