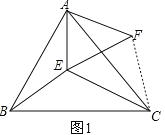
【题目】(1)如图 1 所示,△ ABC 和△ AEF 为等边三角形,点 E 在△ ABC 内部,且 E 到点 A、B、C 的距离分别为 3、4、5,求∠AEB 的度数.
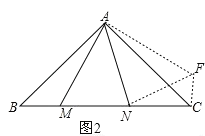
(2)如图 2,在△ ABC 中,∠CAB=90°,AB=AC,M、N 为 BC 上的两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°,得到△ACF.求证:MN![]() = NC
= NC![]() +BM
+BM![]() (提示:旋转前后的图形全等)
(提示:旋转前后的图形全等)
参考答案:
【答案】(1)∠AEB=150°;(2)见解析.
【解析】
(1)根据等边三角形的性质得出AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,求出∠BAE=∠CAF,证出△BAE≌△CAF,得出CF=BE=4,∠AEB=∠AFC,求出CE2=EF2+CF2,得出∠CFE=90°,即可得出结果;
(2)根据将△ABM绕A点逆时针旋转90°,得到△ACF,可知AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,求出∠NAF=∠MAN,证出△MAN≌△FAN,得出MN=FN,求出∠FCN=90°,由勾股定理得出NF2=CF2+CN2即可解决问题.
解:(1)如图1所示:
∵△ABC和△AEF为等边三角形,
∴AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,
∴∠BAE=∠CAF=60°∠CAE,
在△BAE和△CAF中,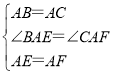 ,
,
∴△BAE≌△CAF(SAS),
∴CF=BE=4,∠AEB=∠AFC,
∴EF=3,CE=5,
∴CE2=EF2+CF2,
∴∠CFE=90°
∵∠AFE=60°,
∴∠AFC=90°+60°=150°,
∴∠AEB=∠AFC=150°;
(2)如图2所示:
∵将△ABM绕A点逆时针选择90°,得到△ACF,
∴AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,
∵∠BAC=90°,∠MAN=45°,
∴∠NAF=∠CAN+∠FAC=∠CAN+∠BAM=90°45°=45°=∠MAN,
在△MAN和△FAN中,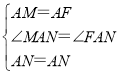 ,
,
∴△MAN≌△FAN(SAS),
∴MN=FN,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵∠B=∠ACF,
∴∠ACF=45°,
∴∠FCN=90°,
由勾股定理得:NF2=CF2+CN2,
∵CF=BM,NF=MN,
∴MN2=NC2+BM2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中, ,
, ,动点
,动点 在
在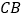 的延长线上运动,动点
的延长线上运动,动点 在
在 的
的延长线上运动,且保持
 的值为
的值为 .设
.设 ,
,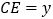 .
. 求
求 与
与 之间的函数关系式;
之间的函数关系式; 用描点法画出
用描点法画出 中函数的图象;
中函数的图象; 已知直线
已知直线 与
与 中函数图象的交点坐标是
中函数图象的交点坐标是 ,求
,求 的值;
的值; 求
求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,且∠EAF=60°,BE=2cm,DF=3cm,试求平行四边形ABCD的周长及面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程.
(1)x2﹣x﹣1=0;
(2)x2﹣2x=2x+1;
(3)x(x﹣2)﹣3x2=﹣1;
(4)(x+3)2=(1﹣2x)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=
 c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+
 cx+b=0必有实数根;
cx+b=0必有实数根;若x=1是“勾系一元二次方程”ax+
 cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是 ,求△ABC面积.
,求△ABC面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )

A.
 B.
B.  C. 5 D.
C. 5 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】动手操作:如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=4,点D为边AC上一动点,DE⊥AB交AB于点E,将∠A沿直线DE折叠,点A的对应点为F.当△DFC是直角三角形时,AD的长为_____.
相关试题

