【题目】如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D在AB上,点E与点C在AB的两侧,连接BE,CD,点M、N分别是BE、CD的中点,连接MN,AM,AN. 下列结论:①△ACD≌△ABE;②△ABC∽△AMN;③△AMN是等边三角形;④若点D是AB的中点,则S△ABC=2S△ABE .
其中正确的结论是 . (填写所有正确结论的序号)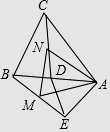
参考答案:
【答案】①②④
【解析】解:①在△ACD和△ABE中, ∵ 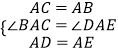 ,
,
∴△ACD≌△ABE(SAS),
所以①正确;②∵△ACD≌△ABE,
∴CD=BE,∠NCA=∠MBA,
又∵M,N分别为BE,CD的中点,
∴CN=BM,
在△ACN和△ABM中,
∵ 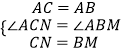 ,
,
∴△ACN≌△ABM,
∴AN=AM,∠CAN∠BAM,
∴∠BAC=∠MAN,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠ABC∠AMN,
∴△ABC∽△AMN,
所以②正确;③∵AN=AM,
∴△AMN为等腰三角形,
所以③不正确;④∵△ACN≌△ABM,
∴S△ACN=S△ABM ,
∵点M、N分别是BE、CD的中点,
∴S△ACD=2S△ACN , S△ABE=2S△ABM ,
∴S△ACD=S△ABE ,
∵D是AB的中点,
∴S△ABC=2S△ACD=2S△ABE ,
所以④正确;
本题正确的结论有:①②④;
所以答案是:①②④.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国东汉初年编订的一部数学经典著作
 在它的“方程”一章里,一次方程组是由算筹布置而成的
在它的“方程”一章里,一次方程组是由算筹布置而成的 九章算术
九章算术 中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图
中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图 图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项
图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项 把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是
把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是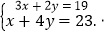 类似地,图2所示的算筹图我们可以表述为______.
类似地,图2所示的算筹图我们可以表述为______.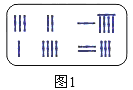
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究证明:
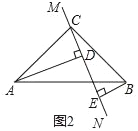
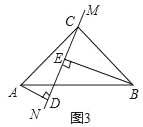
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E,当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)发现探究:
当直线MN绕点C旋转到图2的位置时,(1)中的结论是否成立,如果不成立,DE、AD、BE应满足的关系是_____.
(3)解决问题:
当直线MN绕点C旋转到图3的位置时,若BE=8,AD=2,请直接写出DE的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】有三张正面分别标有数字﹣3,1,3的不透明卡片,它们除数字外都相同,现将它们背面朝上,洗匀后从三张卡片中随机地抽取一张,放回卡片洗匀后,再从三张卡片中随机地抽取一张.
(1)试用列表或画树状图的方法,求两次抽取的卡片上的数字之积为负数的概率;
(2)求两次抽取的卡片上的数字之和为非负数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
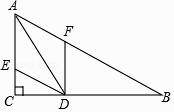
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号) -
科目: 来源: 题型:
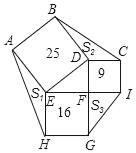
查看答案和解析>>【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
相关试题

